题目内容

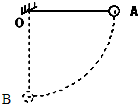
如图所示，长为l的轻细绳，上端固定在天花板上，下端系一质量为m的小球，将小球拉开到绳子绷直且呈水平的A点，无初速度释放小球，空气阻力不计，求：
（1）小球落至最低点B时的速度大小；
（2）小球落至最低点时受到绳子拉力的大小．
（1）球从A点至最低点B过程机械能守恒，设落至最低点时速度为v，则：
mgl=
1
2
mv2
得：v=
2gl
；
小球落至最低点时的速度大小为
2gl
；
（2）至最低点时：
小球受合力F合=F-mg=m
v2
l

得：F=3mg
由牛顿第三定律可得绳子受到的拉力为3mg．
练习册系列答案
相关题目
在下列物体运动中，机械能守恒的是（　　）
A．加速向上运动的运载火箭
B．被匀速吊起的集装箱
C．光滑曲面上自由运动的物体
D．在粗糙水平面上运动的物体
如图所示，一轻质弹簧左端固定在长木块M的左端，右端与小物块m连接，且m与M及M与地面间接触面均光滑，开始时，m和M均处于静止状态，现同时对m、M施加等大反向的水平恒力F1和F2．两物体开始运动后的整个过程中，对m、M和弹簧组成的系统（整个过程中弹簧形变量不超过其弹性限度，M足够长），下列说法正确的是（　　）
A．由于F1、F2等大反向，故两力对系统所做功的代数和为零
B．由于F1、F2都对m、M做正功，故系统动能不断增大
C．当弹簧弹力大小与F1、F2大小相等时，系统动能最大
D．从开始运动到弹簧伸长至最长的过程中，由于F1、F2都对m、M做正功，故系统机械能不断增大
在光滑的水平轨道上有质量为m的物体A，处于静止状态，物体B的质量也为m，由不可伸长的轻绳悬挂于O点，B与轨道接触但不挤压．某时刻开始受到水平方向的恒力F的作用，经过的距离为L时撤掉F，A再运动一段距离后与物体B碰撞，求：
（1）撤掉F时A的速度？F的作用时间？
（2）若A、B发生完全弹性碰撞，绳长为r，则B在碰后的瞬间轻绳受到的拉力？
（3）若A、B发生的碰撞情况是所有可能发生的碰撞情况中的一种，那么绳长满足什么条件才能使B总能完成完整的圆周运动？
甲、乙两球质量相同，悬线一长一短，如将两球从图所示位置，同一水平面无初速释放，不计阻力，则小球通过最低点的时刻?（　　）
A．甲球的动能较乙球大?
B．两球受到的拉力大小相等?
C．两球的向心加速度大小相等?
D．相对同一参考平面，两球机械能相等
一小孩从公园中的光滑滑梯上加速滑下，对于其机械能情况，下列说法中正确的是（　　）
A．重力势能减小，动能不变，机械能减小
B．重力势能减小，动能增加，机械能减小
C．重力势能减小，动能增加，机械能增加
D．重力势能减小，动能增加，机械能不变
如图所示，两质量相同的小球A、B分别用线悬在等高的O1、O2点，A球的悬线比B球的长．把两球的悬线均拉到水平后将小球无初速释放，则经最低点时（以悬点为零势能点）下列说法不正确的是（　　）
A．A球的速度大于B球的速度
B．A球的动能大于B球的动能
C．A球的机械能大于B球的机械能
D．A球的机械能等于B球的机械能
如图所示，在水平地面上固定一个半径为R的半圆形轨道，其中圆弧部分光滑，水平段长为L，一个质量为m的小物块紧靠在被压缩的弹簧最右端，小物块与水平轨道间的动摩擦因数为μ．现突然释放弹簧，让小物块被弹出恰好能够运动到圆弧轨道的最高点A，取g=10m/s2，且弹簧长度忽略不计，求：
（1）小物块在圆弧顶端A处速度大小；
（2）O′点处轨道对小物块的支持力多大；
（3）小物块释放前弹簧具有的弹性势能EP．
一质点在0～6s内竖直向上运动，若取竖直向下为正方向，其加速度一时间图象如图所示，重力加速度g=10m/s2，则下列说法正确的是（　　）
A．在2s～4s内，质点的动能增加
B．在4s～6s内，质点的机械能增加
C．在0～6s内质点的机械能不断增加
D．质点在t=6s时的机械能大于其在2s的机械能

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网