题目内容
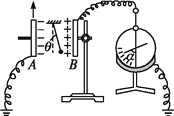
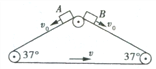
【题目】如图所示，三角形传送带以
的速度逆时针匀速转动，传送带两边倾斜部分的长度都是
，且与水平方向的夹角均为
。现有两个质量均为
的小物体
从传送带顶端都以
的初速度同时沿传送带下滑，物体与传送带间的动摩擦因数都是
。取
， 
。求：
(1) 
两物体到达传送带底端的时间差（结果可用分数表示）；
(2)整个下滑过程中因摩擦产生的总热量
【答案】（1）
（2）220J
【解析】（1）受力分析如图所示；
对A，受到沿着传送带向下的摩擦力，则mgsin37°+μmgcos37°＝ma 解得：a＝12m/s2
设经过时间t1，A与传送带达到共同速度，由运动学公式，得v=v0+at1
得：t1＝
s
此时A下滑的位移x＝
t1＝1m
以后物体与传送带一起匀速下滑到最低端L-x=vt2得：t2=1s
A下滑的时间为：tA＝t1+t2＝1
s
对B受力分析可知，B一直做匀速直线运动，tB＝
＝6s
A、B两物体到达传送带底端的时间差△t＝tBtA＝4
s
（2）A在与传送带相对滑动的过程中，与传送带的相对路程为△x1＝vt1x＝
m
B一直匀速运动，但是与传送带的运动方向相反，故与传送带的相对路程为△x2=vtB+v0tB=36m
因为滑动摩擦力产生热量Q=μmgcos37°（△x1+△x2）=220J
练习册系列答案
相关题目
