题目内容
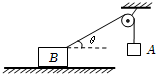如图所示，轻质光滑滑轮两侧用轻绳连着两个物体A与B，物体B放在水平地面上，A、B均静止．已知A和B的质量分别为mA、mB，绳与水平方向的夹角为θ（θ＜90°），重力加速度为g，则物体B受到的摩擦力为mAgcosθ
mAgcosθ
；物体B对地面的压力为mBg-mAgsinθ
mBg-mAgsinθ
．分析：以B为研究对象，分析受力，作出力图．绳子的拉力大小等于A的重力不变．根据平衡条件分析摩擦力和支持力．
解答：解：以B为研究对象，分析受力，作出力图如图所示．
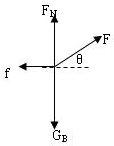
根据平衡条件得：
物体B受到的摩擦力：f=Fcosθ
物体B受到的支持力：FN=mBg-Fsinθ
又F=mAg
得到：f=mAgcosθ，FN=mBg-mAgsinθ．
故答案为：mAgcosθ； mBg-mAgsinθ．
根据平衡条件得：
物体B受到的摩擦力：f=Fcosθ
物体B受到的支持力：FN=mBg-Fsinθ
又F=mAg
得到：f=mAgcosθ，FN=mBg-mAgsinθ．
故答案为：mAgcosθ； mBg-mAgsinθ．
点评：本题采用正交分解法处理力平衡问题，这是物体受多个力作用时常用的方法，中等难度．
练习册系列答案
优学名师名题系列答案
相关题目
如图所示，轻质弹簧的一端固定在墙上，另一端与质量为m的物体A相连，A放在光滑水平面上，有一质量与A相同的物体B，从高h处由静止开始沿光滑曲面滑下，与A相碰后一起将弹簧压缩，弹簧复原过程中某时刻B与A分开且沿原曲面上升．下列说法正确的是（ ）
如图所示，轻质细绳的一端系一质量m=0.01kg的小球，另一端系一光滑小环套在水平轴O上，O到小球的距离d=0.1m，小球跟水平面接触无相互作用力，在球的两侧距球等远处，分别竖立一固定挡板，两挡板相距L=2m．水平面上有一质量为M=0.01kg的小滑块，与水平面间的动摩擦因数μ=0.25，开始时，滑块从左挡板处，以v0=10m/s的初速度向小球方向运动，不计空气阻力，设所有碰撞均无能量损失，小球可视为质点，g=10m/s2．则：
的滑块以
的速度沿光滑水平面运动并压缩弹簧，求(1)弹簧在被压缩过程中最大弹性势能(5分)，(2)当木块的速度减为
时，弹簧具有的弹性势能(5分)。
如图所示，轻质弹簧的一端固定在墙上，另一端与质量为m的物体A相连，A
放在光滑水平面上，有一质量与A相同的物体B，从高h处由静止开始沿光滑曲面滑下，与A相碰后一起将弹簧压缩，弹簧复原过程中某时刻B与A分开且沿原曲面上升．下列说法正确的是 ( )
| A．弹簧被压缩时所具有的最大弹性势能为mgh |
B．弹簧被压缩时所具有的最大弹性势能为 |
C．B能达到的最大高度为 |
D．B能达到的最大高度为 |