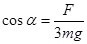题目内容
 如图所示,轻质细绳的一端系一质量m=0.01kg的小球,另一端系一光滑小环套在水平轴O上,O到小球的距离d=0.1m,小球跟水平面接触无相互作用力,在球的两侧距球等远处,分别竖立一固定挡板,两挡板相距L=2m.水平面上有一质量为M=0.01kg的小滑块,与水平面间的动摩擦因数μ=0.25,开始时,滑块从左挡板处,以v0=10m/s的初速度向小球方向运动,不计空气阻力,设所有碰撞均无能量损失,小球可视为质点,g=10m/s2.则:
如图所示,轻质细绳的一端系一质量m=0.01kg的小球,另一端系一光滑小环套在水平轴O上,O到小球的距离d=0.1m,小球跟水平面接触无相互作用力,在球的两侧距球等远处,分别竖立一固定挡板,两挡板相距L=2m.水平面上有一质量为M=0.01kg的小滑块,与水平面间的动摩擦因数μ=0.25,开始时,滑块从左挡板处,以v0=10m/s的初速度向小球方向运动,不计空气阻力,设所有碰撞均无能量损失,小球可视为质点,g=10m/s2.则:(1)在滑块第一次与小球碰撞后的瞬间,悬线对小球的拉力多大?
(2)试判断小球能否完成完整的圆周运动.如能完成,则在滑块最终停止前,小球能完成完整的圆周运动多少次?
分析:(1)根据动能定理求出木块与小球碰撞前的速度,碰撞的过程中无能量损失,根据动量守恒定律和能量守恒定律求出碰后小球的速度,结合牛顿第二定律求出绳子拉力的大小.
(2)根据牛顿第二定律求出小球做圆周运动在最高点的最小速度,通过动能定理求出最后一次碰撞后的速度,抓住碰撞过程中速度交换,对木块全过程运用动能定理,从而得出小球能完成完整圆周运动的次数.
(2)根据牛顿第二定律求出小球做圆周运动在最高点的最小速度,通过动能定理求出最后一次碰撞后的速度,抓住碰撞过程中速度交换,对木块全过程运用动能定理,从而得出小球能完成完整圆周运动的次数.
解答:解:(1)根据动能定理得:-μMg?
=
Mv12-
Mv02
代入数据解得:v1=
m/s.
根据动量守恒定律得:Mv1=Mv1′+mv2
根据能量守恒定律得:
Mv12=
Mv1′2+
mv22.
联立解得:v2=v1=
m/s.
根据牛顿第二定律得:T-mg=m
解得:T=mg+m
=0.1+0.01×
N=9.6N.
(2)能.设第K次碰撞恰能完成完整的圆周运动,
在最高点的临界速度为:v=
根据动能定理得:-mg?2d=
mv2-
mvk2
解得:vK=
…①
木块与小球质量相等,碰撞过程中动量守恒、能量守恒,交换速度,
整个过程中由动能定理得:-(2K-1)μmg
=
m
-
m
…②
由①②得k=10,可知小球能完成完整的圆周运动10次.
答:(1)悬线对小球的拉力为9.6N.
(2)能,小球能完成完整的圆周运动10次.
| L |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:v1=
| 95 |
根据动量守恒定律得:Mv1=Mv1′+mv2
根据能量守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
联立解得:v2=v1=
| 95 |
根据牛顿第二定律得:T-mg=m
| v22 |
| d |
解得:T=mg+m
| v22 |
| d |
| 95 |
| 0.1 |
(2)能.设第K次碰撞恰能完成完整的圆周运动,
在最高点的临界速度为:v=
| gd |
根据动能定理得:-mg?2d=
| 1 |
| 2 |
| 1 |
| 2 |
解得:vK=
| 5gd |
木块与小球质量相等,碰撞过程中动量守恒、能量守恒,交换速度,
整个过程中由动能定理得:-(2K-1)μmg
| L |
| 2 |
| 1 |
| 2 |
| v | 2 K |
| 1 |
| 2 |
| v | 2 0 |
由①②得k=10,可知小球能完成完整的圆周运动10次.
答:(1)悬线对小球的拉力为9.6N.
(2)能,小球能完成完整的圆周运动10次.
点评:本题综合考查动量守恒定律、能量守恒定律、牛顿第二定律和动能定理,综合性较强,对学生的能力要求较高,是道难题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
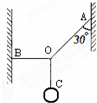 如图所示,轻质细绳将一个小球悬挂起来保持平衡,AO与竖直方向的夹角为30°,此时水平细绳BO上的拉力为F.若保持AO绳的方向不变,将B点向上缓慢移动,使BO绳绕O点瞬时针转过60°角的过程中,F力的大小( )
如图所示,轻质细绳将一个小球悬挂起来保持平衡,AO与竖直方向的夹角为30°,此时水平细绳BO上的拉力为F.若保持AO绳的方向不变,将B点向上缓慢移动,使BO绳绕O点瞬时针转过60°角的过程中,F力的大小( ) 5u
5u B.
B.
 D.
D.