题目内容
7. 某同学根据所学知识设计了如图所示加速器,给质量为m,电量为+q的小球(视为质点)加速,两固定的平行金属板上下放置,板间固定一半径为R的竖直光滑绝缘圆轨道,在轨道最高点和最低点处各有一个感应器(视为质点).某时刻小球以初速度v0从轨道最低点水平向右冲入圆轨道,感应器立刻通过控制电路在两金属板间加上大小恒定的电压,使板间产生方向竖直向上的电场强度E,且qE=2mg,之后小球每经过一次感应器感应器就通过控制电路使电场反向一次:
某同学根据所学知识设计了如图所示加速器,给质量为m,电量为+q的小球(视为质点)加速,两固定的平行金属板上下放置,板间固定一半径为R的竖直光滑绝缘圆轨道,在轨道最高点和最低点处各有一个感应器(视为质点).某时刻小球以初速度v0从轨道最低点水平向右冲入圆轨道,感应器立刻通过控制电路在两金属板间加上大小恒定的电压,使板间产生方向竖直向上的电场强度E,且qE=2mg,之后小球每经过一次感应器感应器就通过控制电路使电场反向一次:(1)要让小球始终不脱离轨道,v0至少为多大?
(2)在v0取(1)临界值情况下,小球转了n圈回到出发点时的速度多大?
(3)若感应器从感知小球到通过控制电路使电场反向,需要反应时间△t,求该加速器能使小球达到的最大速度(小球达最大速度时可近视为作匀速圆周运动).
分析 (1)首先分析小球的受力情况,据圆周运动的临界条件和动能定理求解即可.
(2)据动能定理求出转n圈回到出发点的速度;
(3)据反应时间,分析小球的运动,当小球速度最大时,运动一周的时间为2△t,据此求解即可.
解答 解:(1)以小球为研究对象,受重力和电场力的合力为mg,方向向上,所以要让小球始终不脱离轨道,在低点做圆周运动,即mg=$\frac{m{v}_{0}^{2}}{R}$
解得:v0=$\sqrt{gR}$
(2)小球转一圈时,电场力和重力做的功为:2mgR+6mgR=8mgR
小球转了n圈回到出发点时,据动能定理得:8nmgR=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$
解得:v=$\sqrt{16ngR+gR}$
(3)由于反应时间△t,当小球到达下一个感应器时,小球的速度最大,即小球转动一周的时间为2△t,
此时的速度为:vmax=$\frac{2πR}{2△t}$=$\frac{πR}{△t}$
答:(1)要让小球始终不脱离轨道,v0至少为$\sqrt{gR}$.
(2)在v0取(1)临界值情况下,小球转了n圈回到出发点时的速度$\sqrt{16ngR+gR}$
(3)若感应器从感知小球到通过控制电路使电场反向,需要反应时间△t,该加速器能使小球达到的最大速度$\frac{πR}{△t}$.
点评 本题是信息题,难度较大,关键是类比圆周运动的临界条件是解题的突破口,灵活利用动能定理和反应时间分析小球的最大速度,总之,此题的灵活性很强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列说法中正确的是( )
| A. | 两列波发生干涉时,振动加强的质点位移始终最大 | |
| B. | 无线网络信号能绕过障碍物传递到接收终端,这是利用了衍射原理 | |
| C. | 狭义相对性原理认为,在任何参考系中,物理规律都是相同的 | |
| D. | 观察者相对于频率一定的声源运动时,接收到声波的频率可能发生变化 | |
| E. | 变化电场的周围空间一定会产生磁场 |
18. 两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )
两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )
 两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )
两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )| A. | M点电势为零,N点场强为零 | |
| B. | M点场强为零,N点电势为零 | |
| C. | Q1带负电,Q2带正电,且Q2电荷量较大 | |
| D. | Q1带正电,Q2带负电,且Q2电荷量较大 |
12.如图是某质点的v-t图象,则( )
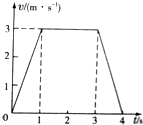

| A. | 在1s到3s时间内质点静止 | |
| B. | 前1s质点做加速运动,最后1s质点做减速运动 | |
| C. | 前1s和最后1s质点的加速度大小均为3m/s2 | |
| D. | 第4s内质点的加速度为0 |
19.(多选)用多用电表的欧姆档测电阻时,下列说法中正确的是( )
| A. | 多用电表的指针指向“0Ω”时,说明通过电流表的电流达到满偏电流 | |
| B. | 测电阻前,把选择开关置于相应的欧姆档,将两表笔直接接触,调整欧姆调零旋钮使指针指向“0Ω” | |
| C. | 用欧姆表“×100”档测电阻时,若指针在“0Ω”附近,应换用“×1k”档 | |
| D. | 测量前,待测电阻必须与其他元件和电源断开 |
16.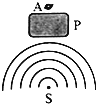 如图,P为桥墩,A为靠近桥墩浮在水面的叶片,波源S连续振动,形成水波,此时叶片A静止不动.为使水波能带动叶片振动,可用的方法是( )
如图,P为桥墩,A为靠近桥墩浮在水面的叶片,波源S连续振动,形成水波,此时叶片A静止不动.为使水波能带动叶片振动,可用的方法是( )
 如图,P为桥墩,A为靠近桥墩浮在水面的叶片,波源S连续振动,形成水波,此时叶片A静止不动.为使水波能带动叶片振动,可用的方法是( )
如图,P为桥墩,A为靠近桥墩浮在水面的叶片,波源S连续振动,形成水波,此时叶片A静止不动.为使水波能带动叶片振动,可用的方法是( )| A. | 提高波源频率 | B. | 降低波源频率 | ||
| C. | 增加波源距桥墩的距离 | D. | 减小波源距桥墩的距离 |
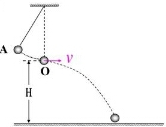 若小球摆到最低点时绳子断裂,小球水平飞出时的离地高度为H,则:
若小球摆到最低点时绳子断裂,小球水平飞出时的离地高度为H,则: 如图所示,坐标平面的第Ⅰ象限内存在电场强度大小为E,方向水平向左的匀强电场,第Ⅱ象限内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.足够长的挡板MN垂直x轴放置,且距原点O的距离为d.若一质量为m、带电荷量为-q的粒子(不计重力)自距原点O为L的A点第一次以大小为v0,方向沿y轴正方向的速度进入磁场,则粒子恰好到达O点而不进入电场.现该粒子仍从A点第二次进入磁场,但初速度大小为2$\sqrt{2}$v0,为使粒子进入电场后能垂直打在挡板上,求:
如图所示,坐标平面的第Ⅰ象限内存在电场强度大小为E,方向水平向左的匀强电场,第Ⅱ象限内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.足够长的挡板MN垂直x轴放置,且距原点O的距离为d.若一质量为m、带电荷量为-q的粒子(不计重力)自距原点O为L的A点第一次以大小为v0,方向沿y轴正方向的速度进入磁场,则粒子恰好到达O点而不进入电场.现该粒子仍从A点第二次进入磁场,但初速度大小为2$\sqrt{2}$v0,为使粒子进入电场后能垂直打在挡板上,求: