题目内容
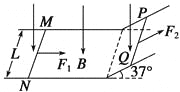
【题目】如图所示,倾角为![]() 的斜面体固定于水平面上,其底端与静止于水平面上的的木板平滑连接,一质量为m=1kg的滑块(可视为质点)恰好能静止于斜面的顶点A,现用一沿斜面向下、大小为4N的恒力F作用于滑块上,滑块运动到斜面底端B时撤去外力。已知斜面高h=1.2m,木板质量M=2kg,滑块与木板间的动摩擦因数是滑块与斜面间动摩擦因素的1/3,木板与水平面间的动摩擦因素
的斜面体固定于水平面上,其底端与静止于水平面上的的木板平滑连接,一质量为m=1kg的滑块(可视为质点)恰好能静止于斜面的顶点A,现用一沿斜面向下、大小为4N的恒力F作用于滑块上,滑块运动到斜面底端B时撤去外力。已知斜面高h=1.2m,木板质量M=2kg,滑块与木板间的动摩擦因数是滑块与斜面间动摩擦因素的1/3,木板与水平面间的动摩擦因素![]() ,
,![]()

(1)求滑块滑到B点时的速度大小v;
(2)要想使滑块不从木板上滑下,求木板的最小长度;
(3)若木板足够长且水平面光滑,求滑块的最终速度大小
【答案】(1)4.2m/s(2)2.52m(3)1.4m/s
【解析】
(1)由题意,恰好能静止于斜面的顶点A,则mgsin370=μ1mgcos370,
解得μ1=0.75
从A到B由动能定理:![]()
解得v=4.2m/s
(2)当滑块滑上木板时,对滑块的加速度:![]() ;
;
对木板:![]()
解得a2=1m/s2
滑块做减速运动,木板做加速运动,当两者共速时:v共=v-a1t=a2t
解得t=1.2s,v共=1.2m/s;
则木板最小长度:![]()
(3)若木板足够长且水平面光滑,当滑块滑上木板时,对滑块的加速度:![]() ;
;
对木板:![]()
解得a3=1.25m/s2
滑块做减速运动,木板做加速运动,当两者共速时:v'共=v-a1t'=a3t'
解得t=1.12s,v'共=1.4m/s;
滑块的最终速度大小1.4m/s;

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目