题目内容
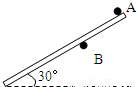
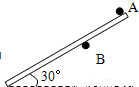
图示A、B分别是固定墙上的两个相同的钉子,一根长2L,质量为m,质量分布均匀的细杆搁在两钉子间处于静止状态,钉子与棒间的滑动摩擦系数为0.5.开始时AB间距离为2/3L,杆的上端恰好在A点,且杆与水平方向的夹角为30°.则B点受到的弹力为 N,如果细杆与水平方向保持30°不变,钉子B沿着杆方向向下改变位置,则B移动到距A L的距离处时,杆不再能保持平衡.
【答案】分析:先对杆受力分析,以A点为支点,根据力矩的平衡条件列式可以求出B钉对杆的支持力;
第二空同样先对杆受力分析,先用A点为支持点,根据力矩的平衡条件列式;再用B点为支持点,根据力矩的平衡条件列式;最后再根据共点力平衡条件列式;联立方程组求解即可.
解答:解:先对杆受力分析,如图
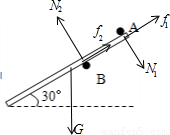
以A点为支点,根据力矩的平衡条件,有
mg(Lcos30°)=N2( )L
)L
解得
N2=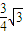 mg
mg
物体恰好滑动时,设B与A相距x,受力分析,同上图
根据力矩平衡条件,有
以A为支持点 mg(Lcos30°)=N2x ①
以B为支持点 mg(l-x)cos30°=N1x ②
根据共点力平衡条件,沿着杆子的方向有
mgsin30°-μN1-μN2=0 ③
由①②③三式,可解得
x=(4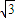 -6)L≈0.93L
-6)L≈0.93L
故答案为: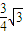 mg,(4
mg,(4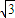 -6).
-6).
点评:本题关键对物体受力分析后,根据共点力平衡条件和力矩平衡条件连列求解.
第二空同样先对杆受力分析,先用A点为支持点,根据力矩的平衡条件列式;再用B点为支持点,根据力矩的平衡条件列式;最后再根据共点力平衡条件列式;联立方程组求解即可.
解答:解:先对杆受力分析,如图

以A点为支点,根据力矩的平衡条件,有
mg(Lcos30°)=N2(
 )L
)L解得
N2=
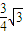 mg
mg物体恰好滑动时,设B与A相距x,受力分析,同上图
根据力矩平衡条件,有
以A为支持点 mg(Lcos30°)=N2x ①
以B为支持点 mg(l-x)cos30°=N1x ②
根据共点力平衡条件,沿着杆子的方向有
mgsin30°-μN1-μN2=0 ③
由①②③三式,可解得
x=(4
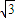 -6)L≈0.93L
-6)L≈0.93L故答案为:
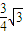 mg,(4
mg,(4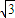 -6).
-6).点评:本题关键对物体受力分析后,根据共点力平衡条件和力矩平衡条件连列求解.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
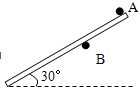 (2011?崇明县二模)图示A、B分别是固定墙上的两个相同的钉子,一根长2L,质量为m,质量分布均匀的细杆搁在两钉子间处于静止状态,钉子与棒间的滑动摩擦系数为0.5.开始时AB间距离为2/3L,杆的上端恰好在A点,且杆与水平方向的夹角为30°.则B点受到的弹力为
(2011?崇明县二模)图示A、B分别是固定墙上的两个相同的钉子,一根长2L,质量为m,质量分布均匀的细杆搁在两钉子间处于静止状态,钉子与棒间的滑动摩擦系数为0.5.开始时AB间距离为2/3L,杆的上端恰好在A点,且杆与水平方向的夹角为30°.则B点受到的弹力为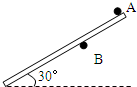 图示A、B分别是固定墙上的两个相同的钉子,一根长2L,质量为m,质量分布均匀的细杆搁在两钉子间处于静止状态,开始时AB间距离为2/3L,杆的上端恰好在A点,且杆与水平方向的夹角为30°.
图示A、B分别是固定墙上的两个相同的钉子,一根长2L,质量为m,质量分布均匀的细杆搁在两钉子间处于静止状态,开始时AB间距离为2/3L,杆的上端恰好在A点,且杆与水平方向的夹角为30°.