题目内容
在真空中波长为400nm的紫光,以53°的入射角从空气射入某种透明液体中,折射角为37°(sin37°=0.6,sin53°=0.8))求:
(1)该液体对紫光的折射率.
(2)紫光在该液体中的传播速度.
(3)紫光在该液体中的波长.
(1)该液体对紫光的折射率.
(2)紫光在该液体中的传播速度.
(3)紫光在该液体中的波长.
分析:(1)根据折射定律求出该液体对紫光的折射率.
(2)紫光在该液体中的传播速度由公式v=
求解.
(3)紫光从真空射入液体中时频率不变,根据波速公式v=λf,求解紫光在该液体中和真空波长之比,即可求解.
(2)紫光在该液体中的传播速度由公式v=
| c |
| n |
(3)紫光从真空射入液体中时频率不变,根据波速公式v=λf,求解紫光在该液体中和真空波长之比,即可求解.
解答:解:(1)根据折射定律得:
该液体对紫光的折射率:n=
=
=
(2)由n=
得:
紫光在该液体中的传播速度:v=
=
m/s=2.25×108m/s
(3)紫光从真空射入液体中时频率不变.
设c是真空中的光速,λ0是真空中的波长,λ是紫光在该液体中的波长.
由波速公式v=λf和n=
得:n=
=
∴λ=
=
nm=300nm
答:
(1)该液体对紫光的折射率为
.
(2)紫光在该液体中的传播速度为2.25×108m/s.
(3)紫光在该液体中的波长为300nm.
该液体对紫光的折射率:n=
| sin53° |
| sin37° |
| 0.8 |
| 0.6 |
| 4 |
| 3 |
(2)由n=
| c |
| v |
紫光在该液体中的传播速度:v=
| c |
| n |
| 3×108 | ||
|
(3)紫光从真空射入液体中时频率不变.
设c是真空中的光速,λ0是真空中的波长,λ是紫光在该液体中的波长.
由波速公式v=λf和n=
| c |
| v |
| λ0f |
| λf |
| λ0 |
| λ |
∴λ=
| λ0 |
| n |
| 400 | ||
|
答:
(1)该液体对紫光的折射率为
| 4 |
| 3 |
(2)紫光在该液体中的传播速度为2.25×108m/s.
(3)紫光在该液体中的波长为300nm.
点评:解决本题的关键掌握光的折射定律和公式v=
,抓住光的频率不变的特性,会推导真空中波长与介质中波长的关系式:n=
.
| c |
| n |
| λ0 |
| λ |

练习册系列答案
相关题目
| (2008?蓟县二模)表1给出了各色光在真空中的波长和频率,表2给出了几种金属的极限频率υ0和极限波长λ0,请你判断下列说法正确的是( ) 表1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
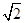 倍,且与MN所成的角α=30°,求:此透明体折射率和单色光在透明球体中的波长。
倍,且与MN所成的角α=30°,求:此透明体折射率和单色光在透明球体中的波长。