题目内容
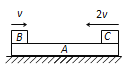
【题目】质量为m的长木板A静止在光滑水平面上，另两个质量也是m的铁块B、C同时从A的左右两端滑上A的上表面，初速度大小分别为v和2v，B、C与A间的动摩擦因数均为μ。已知以后的运动过程中B、C始终没有相撞。
（1）为使B、C不相撞，A木板至少多长。
（2）试求从B、C滑上长木板A后，到不再有相对运动的这段时间内A的位移。
（3）B、C在A上相对滑动的距离之比dB∶dC
【答案】（1）
(2) x=v2/9g(3) 3∶11
【解析】由动量守恒
求出A、B、C最终的共同速度
（1）全过程系统动能的损失都将转化为系统的内能，而摩擦生热
由能量守恒定律列式： 
解得： 
.这就是A木板应该具有的最小长度。
（2)B、C都相对于A滑动时，A所受合力为零，保持静止。B刚好相对于A 静止时，C速度为v，A开向左做匀加速运动，这段加速经历时间为
物体A的位移
(3)第一阶段B对A的位移就是对地的位移： 
，
这段时间为
C的平均速度是其3倍因此C对A的位移是其3倍： 
；
第二阶C平均速度是
，时间为
，
C对地位移是
，A对地位移是
，
因此C相对于A位移是
，
故B、C与A间的相对位移大小依次是
和
，
因此dB∶dC=3∶11.
练习册系列答案
相关题目
