题目内容
6.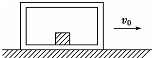 如图所示,一个质量为M木箱原来静止在光滑水平面上,木箱内粗糙的底板上放着一个质量为m的小木块,m=0.25M,现使木箱获得一个向右的初速度v0,则( )
如图所示,一个质量为M木箱原来静止在光滑水平面上,木箱内粗糙的底板上放着一个质量为m的小木块,m=0.25M,现使木箱获得一个向右的初速度v0,则( )| A. | 木箱运动和小木块最终都静止 | |
| B. | 小木块最终速度大小为4v0,方向向右 | |
| C. | 木箱最终速度大小为0.8v0,方向向右 | |
| D. | 如果小木块与木箱的左壁碰撞后相对木箱静止,则二者将一起向左运动 |
分析 本题中物体系统在光滑的平面上滑动,系统所受外力的合力为零,故系统动量始终守恒,而由于系统内部存在摩擦力,阻碍物体间的相对滑动,最终两物体应该相对静止,一起向右运动.由动量守恒求出最终共同速度.
解答 解:A、系统所受外力的合力为零,动量守恒,初状态木箱有向右的动量,小木块动量为零,故系统总动量向右,系统内部存在摩擦力,阻碍两物体间的相对滑动,最终相对静止,由于系统的总动量守恒,不管中间过程如何相互作用,根据动量守恒定律,最终两物体以相同的速度一起向右运动.故AD错误;
BC、最终两物体速度相同,由动量守恒得:Mv0=(m+M)v,则得 v=$\frac{M{v}_{0}}{m+M}$=$\frac{M}{1.25M}$v0=0.8v0,方向向右,故C正确.B错误;
故选:C.
点评 对于动量守恒定律的应用问题,由于不需要涉及中间过程,特别是对于多次碰撞问题,解题特别方便,要能灵活的选用过程.

练习册系列答案
相关题目
17.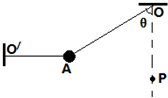 两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )
两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )
 两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )
两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )| A. | 水平细线O′A剪断后的瞬间,OA细线拉力为$\frac{mg}{2}$ | |
| B. | 水平细线O′A剪断后的瞬间,小球A的加速度方向水平向右 | |
| C. | 细线碰到P后的瞬间,OA细线拉力为5mg | |
| D. | 细线碰到P后恰能作完整的圆周运动 |
1.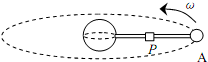 纳米材料的抗拉强度几乎比钢材还高出100倍,使人们设想的太空电梯成为可能.其工作原理是从同步卫星高度的太空站竖直放下由纳米材料做成的太空电梯,固定在赤道上,这样太空电梯随地球一起旋转,如图所示.关于太空电梯仓停在太空电梯中点P时,下列对于太空电梯仓说法正确的是( )
纳米材料的抗拉强度几乎比钢材还高出100倍,使人们设想的太空电梯成为可能.其工作原理是从同步卫星高度的太空站竖直放下由纳米材料做成的太空电梯,固定在赤道上,这样太空电梯随地球一起旋转,如图所示.关于太空电梯仓停在太空电梯中点P时,下列对于太空电梯仓说法正确的是( )
 纳米材料的抗拉强度几乎比钢材还高出100倍,使人们设想的太空电梯成为可能.其工作原理是从同步卫星高度的太空站竖直放下由纳米材料做成的太空电梯,固定在赤道上,这样太空电梯随地球一起旋转,如图所示.关于太空电梯仓停在太空电梯中点P时,下列对于太空电梯仓说法正确的是( )
纳米材料的抗拉强度几乎比钢材还高出100倍,使人们设想的太空电梯成为可能.其工作原理是从同步卫星高度的太空站竖直放下由纳米材料做成的太空电梯,固定在赤道上,这样太空电梯随地球一起旋转,如图所示.关于太空电梯仓停在太空电梯中点P时,下列对于太空电梯仓说法正确的是( )| A. | 处于平衡状态 | B. | 速度比同步卫星大 | ||
| C. | 向心加速度比同高度卫星的小 | D. | 处于完全失重状态 |
11.下列有关四幅图的说法中正确的是( )
| A. | 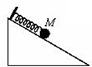 粗糙斜面上的金属球M在弹簧的作用下运动,该运动是简谐运动 | |
| B. | 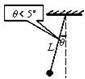 单摆的摆长为L,摆球的质量为m、位移为x,此时回复力为F=-$\frac{mg}{L}$x | |
| C. | 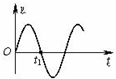 作简谐运动的某质点在t1时刻速度与加速度方向都发生了变化 | |
| D. | 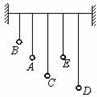 在张紧的绳子上悬挂5个摆,当A摆振动的时候,通过绳使其余各摆做受迫振动,只有E摆振动周期等于A摆振动周期 |
18.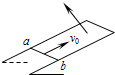 足够长的粗糙U形金属导轨与水平面成θ角,宽度为L,电阻不计.匀强磁场磁感应强度大小为B,方向垂直于导轨平面向上,如图所示.质量为m、电阻为R的金属棒ab从导轨上的某点以初速度v0冲上金属导轨,从冲上导轨到停止运动的过程中,根据题中给定条件可求得的物理量是( )
足够长的粗糙U形金属导轨与水平面成θ角,宽度为L,电阻不计.匀强磁场磁感应强度大小为B,方向垂直于导轨平面向上,如图所示.质量为m、电阻为R的金属棒ab从导轨上的某点以初速度v0冲上金属导轨,从冲上导轨到停止运动的过程中,根据题中给定条件可求得的物理量是( )
 足够长的粗糙U形金属导轨与水平面成θ角,宽度为L,电阻不计.匀强磁场磁感应强度大小为B,方向垂直于导轨平面向上,如图所示.质量为m、电阻为R的金属棒ab从导轨上的某点以初速度v0冲上金属导轨,从冲上导轨到停止运动的过程中,根据题中给定条件可求得的物理量是( )
足够长的粗糙U形金属导轨与水平面成θ角,宽度为L,电阻不计.匀强磁场磁感应强度大小为B,方向垂直于导轨平面向上,如图所示.质量为m、电阻为R的金属棒ab从导轨上的某点以初速度v0冲上金属导轨,从冲上导轨到停止运动的过程中,根据题中给定条件可求得的物理量是( )| A. | 安培力对ab棒所做的功 | |
| B. | ab棒所受的合外力做的功 | |
| C. | 刚冲上导轨的瞬间金属棒所受安培力大小 | |
| D. | 流过ab棒的电量 |
15.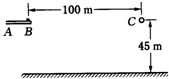 如图枪管AB对准小球C,A、B、C在同一水平面上,枪管和小球距地面的高度为45m.已知BC=100m,当子弹射出枪口时的速度v0=50m/s时,子弹恰好能在C下落20m时击中C.现其他条件不变,只改变子弹射出枪口时的速度v0,则(不计空气阻力,取g=10m/s2)( )
如图枪管AB对准小球C,A、B、C在同一水平面上,枪管和小球距地面的高度为45m.已知BC=100m,当子弹射出枪口时的速度v0=50m/s时,子弹恰好能在C下落20m时击中C.现其他条件不变,只改变子弹射出枪口时的速度v0,则(不计空气阻力,取g=10m/s2)( )
 如图枪管AB对准小球C,A、B、C在同一水平面上,枪管和小球距地面的高度为45m.已知BC=100m,当子弹射出枪口时的速度v0=50m/s时,子弹恰好能在C下落20m时击中C.现其他条件不变,只改变子弹射出枪口时的速度v0,则(不计空气阻力,取g=10m/s2)( )
如图枪管AB对准小球C,A、B、C在同一水平面上,枪管和小球距地面的高度为45m.已知BC=100m,当子弹射出枪口时的速度v0=50m/s时,子弹恰好能在C下落20m时击中C.现其他条件不变,只改变子弹射出枪口时的速度v0,则(不计空气阻力,取g=10m/s2)( )| A. | v0=20 m/s时,子弹能击中小球 | |
| B. | v0=40 m/s时,子弹能击中小球 | |
| C. | v0=30 m/s时,子弹能击中小球 | |
| D. | 以上的三个v0值,子弹可能都不能击中小球 |
14.关于向心力说法正确的是( )
| A. | 物体因为圆周运动才受到向心力 | |
| B. | 向心力不改变圆周运动物体速度的大小 | |
| C. | 作匀速圆周运动的物体其向心力是不变的 | |
| D. | 向心力就是做圆周运动的物体所受到的合外力 |
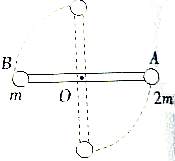 如图所示,在一长为2L不可伸长的轻杆两端各固定一质量为2m与m的小球A、B,系统可绕过轻杆的中点且垂直纸面的固定转轴O转动,初始时轻杆处于水平状态,无初速度释放后轻杆转动,当轻杆转至竖直位置时,求小球A的速率.
如图所示,在一长为2L不可伸长的轻杆两端各固定一质量为2m与m的小球A、B,系统可绕过轻杆的中点且垂直纸面的固定转轴O转动,初始时轻杆处于水平状态,无初速度释放后轻杆转动,当轻杆转至竖直位置时,求小球A的速率.