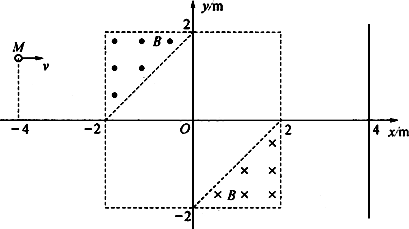
题目内容

如图19-3-3在匀强磁场中的A点，有一个静止的原子核，当它发生哪一种衰变时，射出的粒子以及新核的轨道才做如图的圆周运动，并确定它们环绕的方向，若两圆的半径之比是44∶1，这个放射性元素原子核的原子序数是多少？

图19-3-3

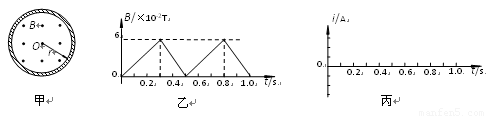
解析：因为原子核衰变时，遵守动量守恒定律，由原于核的初态是静止的，可以判定：衰变时射出的粒子与新核的动量大小相等，方向相反.

设带电粒子质量为m，在磁感应强度为B的磁场中，以速度v做匀速圆周运动，则其运动半径为R=.

由衰变时动量守恒知射出粒子动量m1v1等于新核动量m2v2，而B相同，所以R与q成反比，可判定出衰变射出粒子运动轨道半径大，新核半径小.在A点利用左手定则可判断出新核反冲速度方向，判断出发射粒子的速度方向，即确定粒子的种类和衰变的类型.

由可从发射粒子的电荷数确定新核的电荷数，由于衰变过程中电荷数守恒，可求出原来放射性元素原子核的电荷数即它的原子序数.

由R∝知大圆是发射出粒子的轨迹，小圆则是新核轨迹.

根据左手定则判断：在A点发射出的粒子是负电子，

它初速度水平向左，沿圆轨道顺时针方向旋转.新核初速水平向右，沿圆轨道逆时针旋转.

由于

q1=e，电荷数是1，所以q2=44e，电荷数是44，根据电荷守恒定律，原来的放射性元素原子核的原子序数是45，它发生的是β衰变，电子顺时针方向做匀速圆周运动，新核逆时针做匀速圆周运动.

答案：45

练习册系列答案
相关题目

如图所示，在直角坐标系的第Ⅱ象限和第Ⅳ象限中的直角三角形区域内，分布着磁感应强度均为B＝5.0×10－3 T的匀强磁场，方向分别垂直纸面向外和向里．质量为m＝6.64×10－27 kg、电荷量为q＝＋3.2×10－19 C的α粒子(不计α粒子重力)，由静止开始经加速电压为U＝1205 V的电场(图中未画出)加速后，从坐标点M(－4，)处平行于x轴向右运动，并先后通过两个匀强磁场区域．

(1)请你求出α粒子在磁场中的运动半径；

(2)你在图中画出α粒子从直线x＝－4到直线x＝4之间的运动轨迹，并在图中标明轨迹与直线x＝4交点的坐标；

(3)求出α粒子在两个磁场区域偏转所用的总时间．

如图所示，在直角坐标系的第Ⅱ象限和第Ⅳ象限中的直角三角形区域内，分布着磁感应强度均为B＝5.0×10－3 T的匀强磁场，方向分别垂直纸面向外和向里．质量为m＝6.64×10－27 kg、电荷量为q＝＋3.2×10－19 C的α粒子(不计α粒子重力)，由静止开始经加速电压为U＝1205 V的电场(图中未画出)加速后，从坐标点M(－4，)处平行于x轴向右运动，并先后通过两个匀强磁场区域．

(1)请你求出α粒子在磁场中的运动半径；

(2)你在图中画出α粒子从直线x＝－4到直线x＝4之间的运动轨迹，并在图中标明轨迹与直线x＝4交点的坐标；

(3)求出α粒子在两个磁场区域偏转所用的总时间．

一个半径r=0.10m的闭合导体圆环，圆环单位长度的电阻R0=1.0×10-2 W×m-1。如图19甲所示，圆环所在区域存在着匀强磁场，磁场方向垂直圆环所在平面向外，磁感应强度大小随时间变化情况如图19乙所示。（1）分别求在0~0.3 s和0.3 s~0.5s 时间内圆环中感应电动势的大小；（2）分别求在0~0.3 s和0.3 s~0.5s 时间内圆环中感应电流的大小，并在图19丙中画出圆环中感应电流随时间变化的i-t图象（以线圈中逆时针电流为正，至少画出两个周期）；（3）求在0~10s内圆环中产生的焦耳热。

 
如图19-3-3所示，带电粒子在“云室”中运动时，可呈现其运动径迹，将“云室”放在匀强电场中，通过观察分析带电粒子的径迹，可以研究原子核发生衰变的规律.现将一静止的放射性14C放入上述装置中，当它发生衰变时，可能放出α粒子或电子或正电子.所放射的粒子与反冲核经过相等时间所形成的径迹如图19-3-3所示（发生衰变后的瞬间放射出的粒子和反冲核的速度方向与电场强度E垂直，a、b均表示长度）.则

图19-3-3

（1）14C发生衰变时所放射出的粒子是_____________.

（2）14C发生衰变时所放射出粒子的运动轨迹是____________（填“①”或“②”）.

（3）14C的衰变方程是___________.

（4）简要推导发生衰变后的瞬间放射出的粒子与反冲核的动能之比.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网