题目内容
12. 如图所示,质量为m的滑块P(可视为质点)从四分之一光滑圆弧形轨道A上端静止滑下,到达轨道底端时正好无能量损失滑上质量为M长木板Q的右端.A、Q置于水平桌面上,Q上表面水平.Q左侧桌面上有一挡板,Q与挡板之间有一被压缩的理想弹簧,弹簧与Q之间未连接(挡板与弹簧图中均未画出).已知轨道A的半径为R,P与Q上表面之间动摩擦系数μ1=0.5,Q与水平桌面之间动摩擦系数μ2=0.1,M=6m,弹簧弹性势能为7.5mgR.当P滑上Q时,迅速撤去轨道A,弹簧将Q弹离,之后P滑到Q左端时两者速度刚好均为0.试求Q的长度L.
如图所示,质量为m的滑块P(可视为质点)从四分之一光滑圆弧形轨道A上端静止滑下,到达轨道底端时正好无能量损失滑上质量为M长木板Q的右端.A、Q置于水平桌面上,Q上表面水平.Q左侧桌面上有一挡板,Q与挡板之间有一被压缩的理想弹簧,弹簧与Q之间未连接(挡板与弹簧图中均未画出).已知轨道A的半径为R,P与Q上表面之间动摩擦系数μ1=0.5,Q与水平桌面之间动摩擦系数μ2=0.1,M=6m,弹簧弹性势能为7.5mgR.当P滑上Q时,迅速撤去轨道A,弹簧将Q弹离,之后P滑到Q左端时两者速度刚好均为0.试求Q的长度L.
分析 分析清楚滑块与Q的运动过程,应用动能定理可以求出Q的长度L.
解答 解:由题意分析可知,当P在Q上滑行时,
P一直向左运动,Q一直向右运动.
设P在Q上滑行时,其水平位移为x,
根据动能定理有:μ1mgx=mgR,
代入数据解得:x=2R,
设 PQ之间摩擦力对Q做功为W1,有:W1=-μ1mg(L-x),
设Q与水平桌面之间摩擦力对Q做功为W2,则有:W2=-μ2(M+m)g(L-x)
弹簧对Q做功为W3,有:W3=7.5mgR,
对Q运动全过程应用动能定理有:W1+W2+W3=0,
又:M=6m,联立解得:L=8.25R,
答:Q的长度L为8.25R.
点评 本题是一道力学综合题,物体运动过程复杂,分析清楚物体运动过程是正确解题的关键,分析清楚物体运动过程后应用动能定理可以解题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
20.起重机以0.5m/s2的加速度将质量为1 000kg的货物由静止开始匀加速向上提升,g取10m/s2,则在1s内起重机对货物做的功是( )
| A. | 125 J | B. | 2625 J | C. | 2500 J | D. | 2375 J |
7. 均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R,已知M点的场强大小为E,则N点的场强大小为( )
均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R,已知M点的场强大小为E,则N点的场强大小为( )
 均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R,已知M点的场强大小为E,则N点的场强大小为( )
均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R,已知M点的场强大小为E,则N点的场强大小为( )| A. | $\frac{kq}{4{R}^{2}}$-E | B. | $\frac{kq}{4{R}^{2}}$+E | C. | $\frac{kq}{2{R}^{2}}$-E | D. | $\frac{kq}{2{R}^{2}}$+E |
17. 如图所示,在斜面顶端a处以速度va水平抛出一小球,经过时间ta恰好落在斜面底端P处;今在P点正上方与a等高的b处以速度vb水平抛出另一小球,经过时间tb恰好落在斜面的中点Q处.若不计空气阻力,下列关系式正确的是( )
如图所示,在斜面顶端a处以速度va水平抛出一小球,经过时间ta恰好落在斜面底端P处;今在P点正上方与a等高的b处以速度vb水平抛出另一小球,经过时间tb恰好落在斜面的中点Q处.若不计空气阻力,下列关系式正确的是( )
 如图所示,在斜面顶端a处以速度va水平抛出一小球,经过时间ta恰好落在斜面底端P处;今在P点正上方与a等高的b处以速度vb水平抛出另一小球,经过时间tb恰好落在斜面的中点Q处.若不计空气阻力,下列关系式正确的是( )
如图所示,在斜面顶端a处以速度va水平抛出一小球,经过时间ta恰好落在斜面底端P处;今在P点正上方与a等高的b处以速度vb水平抛出另一小球,经过时间tb恰好落在斜面的中点Q处.若不计空气阻力,下列关系式正确的是( )| A. | va=2vb | B. | va=$\sqrt{2}$vb | C. | ta=2tb | D. | ta=$\sqrt{2}$tb |
4.在下面所说的物体运动情况中,不可能出现的是( )
| A. | 物体在某时刻运动速度很大,而加速度为零 | |
| B. | 物体在某时刻运动速度很小,而加速度很大 | |
| C. | 运动的物体在某时刻速度为零,而其加速度不为零 | |
| D. | 作变速直线运动的物体,a方向与v方向相同,当物体a减小时,它的v也减小 |
1.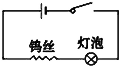 如图所示,在电路中接一段钨丝(从旧日光灯管中取出),闭合开关,灯泡正常发光,当用打火机给钨丝加热时灯泡亮度明显变暗,根据钨丝的上述特性,可用钨丝来制作一个温度传感器,下面的说法中正确的是( )
如图所示,在电路中接一段钨丝(从旧日光灯管中取出),闭合开关,灯泡正常发光,当用打火机给钨丝加热时灯泡亮度明显变暗,根据钨丝的上述特性,可用钨丝来制作一个温度传感器,下面的说法中正确的是( )
 如图所示,在电路中接一段钨丝(从旧日光灯管中取出),闭合开关,灯泡正常发光,当用打火机给钨丝加热时灯泡亮度明显变暗,根据钨丝的上述特性,可用钨丝来制作一个温度传感器,下面的说法中正确的是( )
如图所示,在电路中接一段钨丝(从旧日光灯管中取出),闭合开关,灯泡正常发光,当用打火机给钨丝加热时灯泡亮度明显变暗,根据钨丝的上述特性,可用钨丝来制作一个温度传感器,下面的说法中正确的是( )| A. | 该传感器利用了钨丝的化学性质 | |
| B. | 该传感器利用了钨丝电阻随温度变化而变化的特性 | |
| C. | 该传感器能够把热学量(温度)转换为电学量(电阻) | |
| D. | 该传感器能够把电学量(电阻)转换为热学量(温度) |


