��Ŀ����
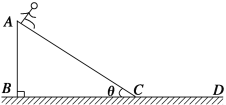
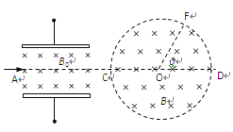
����Ŀ����ͼ��ʾ����һ��ƽ�н����壬�������Ϊ0.05m����ѹΪ10V������֮������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB0=0.1T���������������ƽ�в���ֱ��ֽ�����ͼ���ұ���һ�뾶RΪ0.1m��Բ��ΪO��Բ��������Ҳ������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB=![]() T������ֱ��ֽ�����һ����Ϊm=10-16kg�����������ƽ���ڽ������棬��A�㴹ֱ�ڴų��ķ�������ƽ�н�����֮�䣬��ֱ�����ƽ�н�����֮���������ֱ��CD��������Բ�δų���������Բ������߽��ϵ�F���������֪�ٶȵ�ƫת�� 600����������������
T������ֱ��ֽ�����һ����Ϊm=10-16kg�����������ƽ���ڽ������棬��A�㴹ֱ�ڴų��ķ�������ƽ�н�����֮�䣬��ֱ�����ƽ�н�����֮���������ֱ��CD��������Բ�δų���������Բ������߽��ϵ�F���������֪�ٶȵ�ƫת�� 600����������������
��1�����ٶ�v�Ĵ�С��
��2�����ĵ���q��
��3������Բ�δų��������˶�ʱ��t��
���𰸡���1��2000m/s��2��![]() ��3��
��3��![]() s
s
��������
��1��������������������֮����ֱ�������˵���ܵ��Ĵ�ֱ���˶�����ĵ糡������������ƽ�⣬�ݴ˿ɵ����ӵ��ٶȣ�
��2�������ڴų���������Բ���˶�������ƫת���������ӵ��˶��켣���ɼ��ι�ϵ������ӵ�Բ���˶��뾶��������������������������������̿ɵó����ӵĵ�����
��3������Բ���˶������ڹ�ʽ������ӵĹ켣���Լ�������ӵ��˶�ʱ�䡣
(1) ����ƽ�н�����֮��������ֱ���˶�,����������糡�����,��:
![]()
![]()
����ó�:![]()
(2)��Բ�δų�����,����������Բ���˶�,������������ʽ��ţ�ٵڶ�������:
![]()
![]()
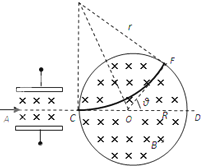
�ɼ��ι�ϵ��:![]()
����� ![]()
(3)��CF��ӦԲ�Ľ�Ϊ![]() ,������Բ�δų��������˶�ʱ��t,
,������Բ�δų��������˶�ʱ��t,
![]()
![]()
����ó�:![]()

 ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д�