题目内容
20.用m表示地球同步卫星的质量,h表示它离地面的高度,R0表示地球的半径,g0表示地球表面的重力加速度,ω0为地球自转的角速度,M表示地球的质量,若该卫星所受地球的万有引力为F,则( )| A. | F=$\frac{GMm}{({R}_{0}+h)^{2}}$ | B. | F=$\frac{m{g}_{0}{{R}_{0}}^{2}}{({R}_{0}+h)^{2}}$ | ||
| C. | F=mω0(R0+h) | D. | F=mω02h |
分析 根据万有引力定律,结合$GM={g}_{0}{{R}_{0}}^{2}$得出万有引力的表达式,或抓住同步卫星的角速度与地球自转的角速度相等,根据万有引力提供向心力求出万有引力的表达式.
解答 解:A、根据万有引力定律得,卫星受到地球的万有引力F=$\frac{GMm}{({R}_{0}+h)^{2}}$,故A正确.
B、根据GM=${g}_{0}{{R}_{0}}^{2}$得,F=$\frac{GMm}{({R}_{0}+h)^{2}}$=$\frac{m{g}_{0}{{R}_{0}}^{2}}{({R}_{0}+h)^{2}}$,故B正确.
C、同步卫星的角速度与地球自转的角速度相等,根据万有引力提供向心力有:F=$m({R}_{0}+h){{ω}_{0}}^{2}$,故C、D错误.
故选:AB.
点评 解决本题的关键掌握“黄金代换式GM=gR2”,并能灵活运用,以及知道同步卫星的角速度与地球自转的角速度相等.

练习册系列答案
相关题目
11. 如图所示,小球的质量为m,自光滑的斜槽的顶端无初速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的动能和重力势能分别是(选取斜槽末端切线所在平面为参考平面)( )
如图所示,小球的质量为m,自光滑的斜槽的顶端无初速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的动能和重力势能分别是(选取斜槽末端切线所在平面为参考平面)( )
 如图所示,小球的质量为m,自光滑的斜槽的顶端无初速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的动能和重力势能分别是(选取斜槽末端切线所在平面为参考平面)( )
如图所示,小球的质量为m,自光滑的斜槽的顶端无初速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的动能和重力势能分别是(选取斜槽末端切线所在平面为参考平面)( )| A. | mg(h+H),mgh | B. | mg(h+H),-mgh | C. | mgH,0 | D. | mgH,-mgH |
15.在竖直上抛运动中,当物体到达最高点时( )
| A. | 速度为零,加速度也为零 | B. | 速度为零,加速度不为零 | ||
| C. | 加速度为零,有向下的速度 | D. | 有向下的速度和加速度 |
5.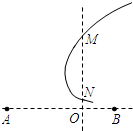 如图所示,真空中有两个等量异种点电荷A、B,M、N、O是AB连线的垂线上的点,且AO>OB.一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,下列判断中正确的是( )
如图所示,真空中有两个等量异种点电荷A、B,M、N、O是AB连线的垂线上的点,且AO>OB.一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,下列判断中正确的是( )
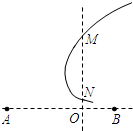 如图所示,真空中有两个等量异种点电荷A、B,M、N、O是AB连线的垂线上的点,且AO>OB.一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,下列判断中正确的是( )
如图所示,真空中有两个等量异种点电荷A、B,M、N、O是AB连线的垂线上的点,且AO>OB.一带负电的试探电荷仅受电场力作用,运动轨迹如图中实线所示,下列判断中正确的是( )| A. | B点电荷一定带正电 | |
| B. | M点的加速度小于N点的加速度 | |
| C. | M点的电势大于N点的电势 | |
| D. | 此试探电荷在M处的速度小于N处的速度 |
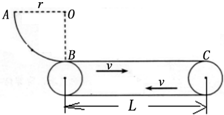 如图所示,固定的光滑$\frac{1}{4}$圆弧轨道AB的半径r=1.25m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.质量m=1kg的小物块(可视为质点)从轨道上的A点由静止释放,到达底端时水平进入轴心距离L=4m的水平传送带,传送带可由一电机驱使沿顺时针匀速转动.已知物体与传送带间的动摩擦因数为μ=0.15.不计物块通过轨道与传送带交接处的动能损失,不计空气阻力,(g=10m/s2)求:
如图所示,固定的光滑$\frac{1}{4}$圆弧轨道AB的半径r=1.25m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.质量m=1kg的小物块(可视为质点)从轨道上的A点由静止释放,到达底端时水平进入轴心距离L=4m的水平传送带,传送带可由一电机驱使沿顺时针匀速转动.已知物体与传送带间的动摩擦因数为μ=0.15.不计物块通过轨道与传送带交接处的动能损失,不计空气阻力,(g=10m/s2)求: 长木板A放在光滑水平面上,质量为m的物块以初速度v0滑上A的水平上表面,它们的v-t图象如图所示,依据图中所给的数据v0、v1、t1及物块质量m,求:
长木板A放在光滑水平面上,质量为m的物块以初速度v0滑上A的水平上表面,它们的v-t图象如图所示,依据图中所给的数据v0、v1、t1及物块质量m,求: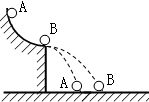 如图所示,有两个大小相等、质量不同的小球A和B,B球静止在光滑圆弧的底端,A球质量为m,从顶端释放,若两球发生弹性碰撞后,它们的落点离平台边缘的水平距离之比为1:3,则B球的质量可能是( )
如图所示,有两个大小相等、质量不同的小球A和B,B球静止在光滑圆弧的底端,A球质量为m,从顶端释放,若两球发生弹性碰撞后,它们的落点离平台边缘的水平距离之比为1:3,则B球的质量可能是( ) 如图所示,两块水平放置、相距为d的长金属板接在电压可调的电源上.两板之间的右侧区域存在方向垂直纸面向里的匀强磁场.将喷墨打印机的喷口靠近上板下表面,从喷口连续不断喷出质量均为m、水平速度均为v0、带相等电荷量的墨滴.调节电源电压至U,墨滴在电场区域恰能沿水平向右做匀速直线运动;进入电场、磁场共存区域后,最终垂直打在下板的M点.
如图所示,两块水平放置、相距为d的长金属板接在电压可调的电源上.两板之间的右侧区域存在方向垂直纸面向里的匀强磁场.将喷墨打印机的喷口靠近上板下表面,从喷口连续不断喷出质量均为m、水平速度均为v0、带相等电荷量的墨滴.调节电源电压至U,墨滴在电场区域恰能沿水平向右做匀速直线运动;进入电场、磁场共存区域后,最终垂直打在下板的M点.