题目内容
16.两个小球A和B在光滑的水平面上沿同一直线运动,A的质量为2kg,速度大小为6m/s,B的质量也为2kg,速度大小为12m/s,求下列两种情况下碰撞后的速度.(1)A和B都向右运动,碰后粘在一起;
(2)A向右运动,B向左运动,碰后粘在一起.
分析 对A、B两球组成的系统研究,运用动量守恒定律求出速度的大小,注意要规定正方向.
解答 解:(1)A、B组成的系统动量守恒,规定向右为正方向,根据动量守恒定律得,
m1v1+m2v2=(m1+m2)v共,
解得${v}_{共}=\frac{2×6+2×12}{4}=9m/s$.
(2)规定向右为正方向,根据动量守恒得,m1v1+m2v2=(m1+m2)v共,
解得:${v}_{共}=\frac{2×6-2×12}{4}=-3m/s$.大小为3m/s,方向向左.
答:(1)A和B都向右运动,碰后粘在一起,碰后速度为9m/s,方向向右;
(2)A向右运动,B向左运动,碰后粘在一起碰后速度大小为3m/s,方向向左.
点评 本题考查了动量守恒定律的基本运用,知道A、B碰撞前后动量守恒,注意公式的矢量性.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
20.用m表示地球同步卫星的质量,h表示它离地面的高度,R0表示地球的半径,g0表示地球表面的重力加速度,ω0为地球自转的角速度,M表示地球的质量,若该卫星所受地球的万有引力为F,则( )
| A. | F=$\frac{GMm}{({R}_{0}+h)^{2}}$ | B. | F=$\frac{m{g}_{0}{{R}_{0}}^{2}}{({R}_{0}+h)^{2}}$ | ||
| C. | F=mω0(R0+h) | D. | F=mω02h |
1.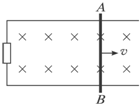 如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过.下列说法中正确的是( )
如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过.下列说法中正确的是( )
 如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过.下列说法中正确的是( )
如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过.下列说法中正确的是( )| A. | 因导体运动而产生的感应电动势称为感生电动势 | |
| B. | 动生电动势的产生与洛伦兹力有关 | |
| C. | 动生电动势的产生与电场力有关 | |
| D. | 动生电动势和感生电动势的产生原因是一样的 |
6.(多选)关于气体分子运动的特点,下列说法正确的是( )
| A. | 气体分子之所以能充满空间,是因为气体分子间相互作用的引力和斥力十分微弱,气体分子可以在空间自由运动 | |
| B. | 每个气体分子的速率都相等 | |
| C. | 每个气体分子的速率都不等,速率很大和速率很小的分子数目很多 | |
| D. | 气体分子速率很大和速率很小的分子数目都很小 |
 刹车距离(即图中“减速过程”所经过的位移),是评价汽车安全性能的一个重要指标.某型号骑车在一段马路上的测试结果是:当骑车以15m/s速度匀速行驶时,从开始到汽车停下的距离是10米.
刹车距离(即图中“减速过程”所经过的位移),是评价汽车安全性能的一个重要指标.某型号骑车在一段马路上的测试结果是:当骑车以15m/s速度匀速行驶时,从开始到汽车停下的距离是10米.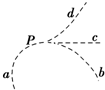 一质点以水平向右的恒定速度通过P点时受到一个恒力F的作用,则此后该质点的运动轨迹不可能是图中的( )
一质点以水平向右的恒定速度通过P点时受到一个恒力F的作用,则此后该质点的运动轨迹不可能是图中的( )