题目内容
如图所示是一个示波管工作原理图,电子经电压U1=4.5×103V加速后以速度V0垂直等间距的进入电压U2=180V,间距为d=1.0cm,板长l=5cm的平行金属板组成的偏转电场,离开电场后打在距离偏转电场s=10cm的屏幕上的P点,(e=1.6×10-19C,m=9.0×10-31kg)
求:
(1)电子进入偏转电场时的速度V0=?
(2)射出偏转电场时速度的偏角tanθ=?
(3)打在屏幕上的侧移位移OP=?

求:
(1)电子进入偏转电场时的速度V0=?
(2)射出偏转电场时速度的偏角tanθ=?
(3)打在屏幕上的侧移位移OP=?
(1)设电子经加速电场U1加速后以速度v0进入偏转电场,由动能定理有
qU1=
mv02,
则有:v0=
=
=4×107m/s;
故电子进入偏转电场的速度v0=4×107m/s;
(2)进入偏转电场后在电场线方向有,a=
经时间t1飞出电场有t1=
,
电场方向的速度vy=at1=
=
=4×106m/s;
设射出偏转电场时速度的偏角为θ,则tanθ=
=
=
(3)飞出电场时偏转量为y1=
at12
由以上各式得y1=
=
=0.25cm;
设电子从偏转场穿出时,沿y方向的速度为vy,穿出后到达屏S所经历的时间为t2,
在此时间内电子在y方向移动的距离为y2,有:vy=at1
t2=
y2=vyt2
由以上各式得
y2=
故电子到达屏S上时,它离O点的距离:y=y1+y2=
(l+s)=
×(0.05+0.1)cm=0.75cm;
答:(1)电子进入偏转电场时的速度4×107m/s;
(2)射出偏转电场时速度的偏角tanθ=
;
(3)打在屏幕上的侧移位移OP=0.75cm.
qU1=
| 1 |
| 2 |
则有:v0=
|
|
故电子进入偏转电场的速度v0=4×107m/s;
(2)进入偏转电场后在电场线方向有,a=
| qU2 |
| md |
经时间t1飞出电场有t1=
| l |
| v0 |
电场方向的速度vy=at1=
| qU2l |
| mdv0 |
| 1.6×10-19×180×0.05 |
| 9×10-31×0.01×4×107 |
设射出偏转电场时速度的偏角为θ,则tanθ=
| vy |
| v0 |
| 4×106 |
| 4×107 |
| 1 |
| 10 |
(3)飞出电场时偏转量为y1=
| 1 |
| 2 |
由以上各式得y1=
U2
| ||
| 4dU1 |
| 180×0.052 |
| 4×0.01×4.5×103 |
设电子从偏转场穿出时,沿y方向的速度为vy,穿出后到达屏S所经历的时间为t2,
在此时间内电子在y方向移动的距离为y2,有:vy=at1
t2=
| s |
| v0 |
y2=vyt2
由以上各式得
y2=
| U2sl |
| 2dU1 |
故电子到达屏S上时,它离O点的距离:y=y1+y2=
| U2l |
| 4dU1 |
| 180×0.05 |
| 4×0.01×4.5×103 |
答:(1)电子进入偏转电场时的速度4×107m/s;
(2)射出偏转电场时速度的偏角tanθ=
| 1 |
| 10 |
(3)打在屏幕上的侧移位移OP=0.75cm.

练习册系列答案
相关题目
 ,丝线长L=40cm,上端系于O点,下端系质量为
,丝线长L=40cm,上端系于O点,下端系质量为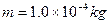 ,带电量为
,带电量为 的小球,将小球从最低点A由静止释放,求:
的小球,将小球从最低点A由静止释放,求:
 ”、“
”、“ ”或“
”或“ ”),c粒子 (填“带正电”、“带负电”或“不带电”)。
”),c粒子 (填“带正电”、“带负电”或“不带电”)。
 =l。不计带电粒子所受重力,求:
=l。不计带电粒子所受重力,求:

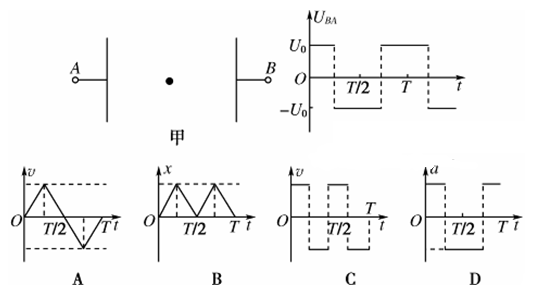
 t,当t=0时,板间有一个电子正好处于静止状态,下面关于电子以后运动情况的判断哪些是正确的( ).
t,当t=0时,板间有一个电子正好处于静止状态,下面关于电子以后运动情况的判断哪些是正确的( ). 时,电子将有最大速度
时,电子将有最大速度 .位移
.位移 .加速度
.加速度 和动能
和动能 四个物理量随时间变化规律的是: ( )
四个物理量随时间变化规律的是: ( )