题目内容
【题目】回旋加速器的工作原理如图甲所示，置于真空中的D形金属盒半径为R，两盒间狭缝的间距为d，磁感应强度为B的匀强磁场与盒面垂直，被加速粒子的质量为m，电荷量为＋q，加在狭缝间的交变电压如图乙所示，电压值的大小为U0.周期T＝
.一束该种粒子在t＝0～
时间内从A处均匀地飘入狭缝，其初速度视为零．现考虑粒子在狭缝中的运动时间，假设能够出射的粒子每次经过狭缝均做加速运动，不考虑粒子间的相互作用．求：
(1)出射粒子的动能Em；
(2)粒子从飘入狭缝至动能达到Em所需的总时间t0；
(3)要使飘入狭缝的粒子中有超过99%能射出，d应满足的条件．
【答案】(1)
(2) 
；(3) d<
【解析】
试题（1）粒子运动半径为R时
且
解得
（2）粒子被加速n次达到动能Em，则Em=nqU0
粒子在狭缝间做匀加速运动，设n次经过狭缝的总时间为Δt
加速度
匀加速直线运动
由
，解得
（3）只有在0~
时间内飘入的粒子才能每次均被加速
则所占的比例为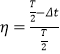
由
,解得
．
练习册系列答案
相关题目
