题目内容
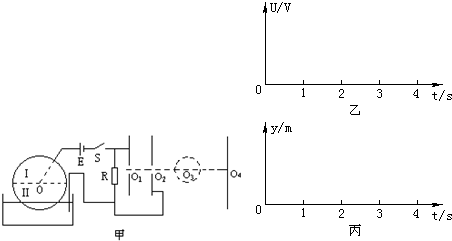
如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的 倍.圆盘可绕O点按顺时针方向转动,且在转动过程中,只要材料进入液体中,材料Ⅰ在O点与液体间的电阻恒为RⅠ=1kΩ,材料Ⅱ在O点与液体间的电阻恒为RⅡ=4kΩ.圆盘通过转轴、导电液体与外电路连接,导线与导电液体电阻不计.电路中电源电动势E=2000V,内阻不计,R=4kΩ.R的两端与两块竖直放置、正对且等大的平行金属板相连,板间距离不计.金属板右侧依次有半径为r/10的圆形匀强磁场区域及竖直放置的荧光屏,已知平行金属板正中央的小孔O1、O2,匀强磁场的圆心O3,荧光屏的中心O4在同一条水平直线上,O3O4=20cm.现有一细束带电粒子从O1点沿O1O2方向进入平行金属板间,初速度及重力不计,比荷
倍.圆盘可绕O点按顺时针方向转动,且在转动过程中,只要材料进入液体中,材料Ⅰ在O点与液体间的电阻恒为RⅠ=1kΩ,材料Ⅱ在O点与液体间的电阻恒为RⅡ=4kΩ.圆盘通过转轴、导电液体与外电路连接,导线与导电液体电阻不计.电路中电源电动势E=2000V,内阻不计,R=4kΩ.R的两端与两块竖直放置、正对且等大的平行金属板相连,板间距离不计.金属板右侧依次有半径为r/10的圆形匀强磁场区域及竖直放置的荧光屏,已知平行金属板正中央的小孔O1、O2,匀强磁场的圆心O3,荧光屏的中心O4在同一条水平直线上,O3O4=20cm.现有一细束带电粒子从O1点沿O1O2方向进入平行金属板间,初速度及重力不计,比荷 .匀强磁场的磁感应强度B=1.0T,圆盘的转动周期T=4s.
.匀强磁场的磁感应强度B=1.0T,圆盘的转动周期T=4s.(1)圆盘处于图示位置时,两平行金属板间的电压是多少?带电粒子打到荧光屏上时距O4点的距离y是多大?
(2)如果圆盘在图位置时为零时刻,在图乙画出平行金属板间电压在一个周期内随时间变化的图象.(可不写计算过程,但需在图上标出具体数值)
(3)在图丙中定性画出电子到达屏上时,它离O4点的距离y随时间的变化图线.

【答案】分析:(1)根据闭合电路欧姆定律求出电阻R两端的电压,从而得出两金属板间的电压大小.根据动能定理求出粒子进入磁场的速度,通过半径公式求出粒子在磁场中运动的半径,结合几何关系求出偏转角的大小,从而得出带电粒子打到荧光屏上时距O4点的距离.
(2)求出各个时间段圆盘部分的并联电阻,通过闭合电路欧姆定律求出平行金属板间电压在一个周期内随时间变化的图象.
(3)粒子的速度越大,偏转角越小,则离O4点的距离y越小.
解答:解:(1)电阻R两端的电压U= .
.
根据动能定理得,qU=
解得v= m/s.
m/s.
粒子在磁场中运动的半径r′=
根据几何关系得,粒子的偏向角为60度.
所以y= .
.
(2)在0-1s内,平行板间的电压为1000V.
在1-2s内,圆盘部分并联电阻为 ,则电阻R两端的电压
,则电阻R两端的电压 .则平行板间的电压为1667V.
.则平行板间的电压为1667V.
 在2-3s内,圆盘部分电阻为1kΩ,则平行板间的电压
在2-3s内,圆盘部分电阻为1kΩ,则平行板间的电压 .
.
在3-4s内,圆盘部分并联电阻为 ,则电阻R两端的电压
,则电阻R两端的电压 .则平行板间的电压为1667V.
.则平行板间的电压为1667V.
所以平行金属板间电压在一个周期内随时间变化的图象如图所示.
(3)粒子速度越大,则偏转角越小,y越小,定性地作出y随时间的变化图线.如图所示.
答:(1)两平行金属板间的电压是1000V,带电粒子打到荧光屏上时距O4点的距离y是
(2)如图所示.
(3)如图所示.
点评:本题考查了闭合电路欧姆定律、动能定理、牛顿第二定律、共点力平衡等知识点,综合性较强,对学生的能力要求较高,需加强训练.
(2)求出各个时间段圆盘部分的并联电阻,通过闭合电路欧姆定律求出平行金属板间电压在一个周期内随时间变化的图象.
(3)粒子的速度越大,偏转角越小,则离O4点的距离y越小.
解答:解:(1)电阻R两端的电压U=
 .
.根据动能定理得,qU=

解得v=
 m/s.
m/s.粒子在磁场中运动的半径r′=

根据几何关系得,粒子的偏向角为60度.
所以y=
 .
.(2)在0-1s内,平行板间的电压为1000V.
在1-2s内,圆盘部分并联电阻为
 ,则电阻R两端的电压
,则电阻R两端的电压 .则平行板间的电压为1667V.
.则平行板间的电压为1667V. 在2-3s内,圆盘部分电阻为1kΩ,则平行板间的电压
在2-3s内,圆盘部分电阻为1kΩ,则平行板间的电压 .
.在3-4s内,圆盘部分并联电阻为
 ,则电阻R两端的电压
,则电阻R两端的电压 .则平行板间的电压为1667V.
.则平行板间的电压为1667V.所以平行金属板间电压在一个周期内随时间变化的图象如图所示.
(3)粒子速度越大,则偏转角越小,y越小,定性地作出y随时间的变化图线.如图所示.
答:(1)两平行金属板间的电压是1000V,带电粒子打到荧光屏上时距O4点的距离y是

(2)如图所示.
(3)如图所示.
点评:本题考查了闭合电路欧姆定律、动能定理、牛顿第二定律、共点力平衡等知识点,综合性较强,对学生的能力要求较高,需加强训练.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
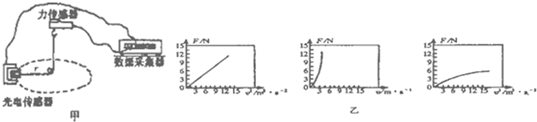
如图甲所示是一个研究向心力与哪些因素有关的DIS实验装置的示意图。其中做匀速圆周运动的圆柱体的质量为m,放置在末画出的圆盘上,圆周轨道的半径为r,力电传感器测定的是向心力,光电传感器测定的是圆柱体的线速度,以下是所得数据和图乙所示的F-v、F-v2、F-v3三个图象。
| v /m·s-1 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| F /N | 0.88 | 2.00 | 3.50 | 5.50 | 7.90 |

【小题2】为了研究F与r的关系,实验时除了要保持圆柱体质量不变外,还应保持物理量_ ___不变。
【小题3】根据你已经学习过的向心力公式以及上面的图线可以推算出,本实验中圆柱体的质量为 kg。
 如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的
如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的
