题目内容
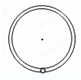
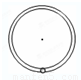
如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多),在圆管中有一直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为7mg。此后小球便作圆周运动,经过半个圆周恰能通过最高点,则此过程中小球克服摩擦力所做的功是

- A.0.5mgR
- B.mgR
- C.2mgR
- D.3mgR
B
试题分析:小球恰好能通过最高点,则小球的速度为零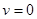 (1)
(1)
小球在最低点,对下管壁的压力为7mg,则有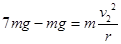 (2)
(2)
所以此过程中重力,摩擦力做负功,根据动能定理可得;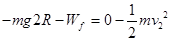
联立解得 ,故B正确,
,故B正确,
考点:本题考查了:圆周运动、牛顿第二定律、
点评:做本题的关键是理解恰好 能通过最高点此时对应的速度
试题分析:小球恰好能通过最高点,则小球的速度为零
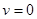 (1)
(1)小球在最低点,对下管壁的压力为7mg,则有
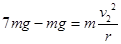 (2)
(2)所以此过程中重力,摩擦力做负功,根据动能定理可得;
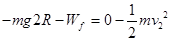
联立解得
 ,故B正确,
,故B正确,考点:本题考查了:圆周运动、牛顿第二定律、
点评:做本题的关键是理解恰好 能通过最高点此时对应的速度

练习册系列答案
相关题目
 如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多),在圆管中有一直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为7mg.此后小球便作圆周运动,经过半个圆周恰能通过最高点,则此过程中小球克服摩擦力所做的功是( )
如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多),在圆管中有一直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为7mg.此后小球便作圆周运动,经过半个圆周恰能通过最高点,则此过程中小球克服摩擦力所做的功是( )