题目内容
18. 如图所示,长L=1m的小车静止在光滑的水平面上,一滑块以v0=3m/s的水平
如图所示,长L=1m的小车静止在光滑的水平面上,一滑块以v0=3m/s的水平速度从小车左端滑入并从小车右端滑出,小车和滑块的质量均为1kg,已知滑块与小车间的动摩擦因数μ=0.2.(g=10m/s2)求:
①滑块离开小车时,滑块和小车的速度分别为多少?
②此过程中,小车受到合外力的冲量?
分析 ①取水平向右为正方向,对滑块滑离小车的过程,根据动量守恒定律及量守恒定律列式即可求解;
②对小车依动量定理列式求解.
解答 解:①取水平向右为正方向.设滑离时,滑块和小车的速度分别为v1,v2,全程,由动量守恒定律有:
mv0=mv1+mv2
依能量守恒定律有:$μmgL=\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}m{{v}_{1}}^{2}-\frac{1}{2}m{{v}_{2}}^{2}$
滑离:v1>v2
解得:v1=2m/s v2=1m/s
②对小车依动量定理有:I=mv2-0
得:I=1Ns,方向水平向右
答:①滑块离开小车时,滑块和小车的速度分别为2m/s和1m/s;
②此过程中,小车受到合外力的冲量大小为1Ns,方向水平向右.
点评 本题主要考查了动量守恒定律及量守恒定律的直接应用,知道当一个系统不受外力或所受外力的矢量和为零,那么这个系统的总动量保持不变.

练习册系列答案
相关题目
8. 下表列出了某种型号轿车的部分数据,如图图为轿车中用于改变车速的档位.手推变速杆到达不同档位可获得不同的运行速度,从“1~5”逐档速度增大,R是倒车档.试问若轿车在额定功率下,要以最大动力上坡,变速杆应推至哪一档?当轿车以最高速度运行时,轿车的牵引力约为多大( )
下表列出了某种型号轿车的部分数据,如图图为轿车中用于改变车速的档位.手推变速杆到达不同档位可获得不同的运行速度,从“1~5”逐档速度增大,R是倒车档.试问若轿车在额定功率下,要以最大动力上坡,变速杆应推至哪一档?当轿车以最高速度运行时,轿车的牵引力约为多大( )
 下表列出了某种型号轿车的部分数据,如图图为轿车中用于改变车速的档位.手推变速杆到达不同档位可获得不同的运行速度,从“1~5”逐档速度增大,R是倒车档.试问若轿车在额定功率下,要以最大动力上坡,变速杆应推至哪一档?当轿车以最高速度运行时,轿车的牵引力约为多大( )
下表列出了某种型号轿车的部分数据,如图图为轿车中用于改变车速的档位.手推变速杆到达不同档位可获得不同的运行速度,从“1~5”逐档速度增大,R是倒车档.试问若轿车在额定功率下,要以最大动力上坡,变速杆应推至哪一档?当轿车以最高速度运行时,轿车的牵引力约为多大( )| 长/mm×宽/mm×高/mm | 4481×1746×1526mm |
| 净重/kg | 1337kg |
| 传动系统 | 前轮驱动与五挡变速 |
| 发动机类型 | 直列4缸 |
| 发动机排量(L) | 2.0L |
| 最高时速(km/h) | 189km/h |
| 100km/h的加速时间(s) | 12s |
| 额定功率(kw) | 108kw |
| A. | “5”档、8000N | B. | “5”档、2000N | C. | “1”档、4000N | D. | “1”档、2000N |
6. 将三个质量均为m的小球a、b、c用细线相连后(bc间无细线相连),再用细线悬挂于O点,如图所示.用力F拉小球c,使三个小球都处于静止状态,且细线Oa与竖直方向的夹角保持为θ=30°,则F的最小值为( )
将三个质量均为m的小球a、b、c用细线相连后(bc间无细线相连),再用细线悬挂于O点,如图所示.用力F拉小球c,使三个小球都处于静止状态,且细线Oa与竖直方向的夹角保持为θ=30°,则F的最小值为( )
 将三个质量均为m的小球a、b、c用细线相连后(bc间无细线相连),再用细线悬挂于O点,如图所示.用力F拉小球c,使三个小球都处于静止状态,且细线Oa与竖直方向的夹角保持为θ=30°,则F的最小值为( )
将三个质量均为m的小球a、b、c用细线相连后(bc间无细线相连),再用细线悬挂于O点,如图所示.用力F拉小球c,使三个小球都处于静止状态,且细线Oa与竖直方向的夹角保持为θ=30°,则F的最小值为( )| A. | mg | B. | 2mg | C. | 1.5mg | D. | $\frac{\sqrt{3}}{2}$mg |
3.“北斗”导航系统是我国自行研发的全球导航系统,它由5颗静止轨道卫星(同步卫星)与30颗非静止轨道卫星组成.已知月球公转周期约为27天,则静止轨道卫星与月球( )
| A. | 角速度之比约为27:1 | B. | 线速度之比约为27:1 | ||
| C. | 半径之比约为1:27 | D. | 向心加速度之比约为1:27 |
10.关于下列现象的说法正确的是( )
| A. |  如图说明分子间存在引力 | |
| B. |  如图在用油膜法测分子大小时,多撒痱子粉比少撒好 | |
| C. |  如图说明,气体压强的大小既与分子动能有关,也与分子的密集程度有关 | |
| D. |  如图水黾停在水面上的原因是水黾受到了水的浮力作用 |
7. 如图所示,将圆柱形强磁铁吸在干电池负极,金属导线折成上端有一支点、下端开口的导线框,使导线框的顶端支点和底端分别与电源正极和磁铁都接触良好但不固定,这样整个线框就可以绕电池轴心旋转起来.下列判断中正确的是( )
如图所示,将圆柱形强磁铁吸在干电池负极,金属导线折成上端有一支点、下端开口的导线框,使导线框的顶端支点和底端分别与电源正极和磁铁都接触良好但不固定,这样整个线框就可以绕电池轴心旋转起来.下列判断中正确的是( )
 如图所示,将圆柱形强磁铁吸在干电池负极,金属导线折成上端有一支点、下端开口的导线框,使导线框的顶端支点和底端分别与电源正极和磁铁都接触良好但不固定,这样整个线框就可以绕电池轴心旋转起来.下列判断中正确的是( )
如图所示,将圆柱形强磁铁吸在干电池负极,金属导线折成上端有一支点、下端开口的导线框,使导线框的顶端支点和底端分别与电源正极和磁铁都接触良好但不固定,这样整个线框就可以绕电池轴心旋转起来.下列判断中正确的是( )| A. | 线框能旋转起来,是因为电磁感应 | |
| B. | 俯视观察,线框沿逆时针方向旋转 | |
| C. | 电池输出的电功率大于线框旋转的机械功率 | |
| D. | 旋转达到稳定时,线框中电流比刚开始转动时的大 |
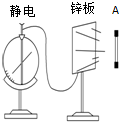 如图所示,一静电计与锌板相连,在A处用一紫外灯照射锌板,关灯后,指针保持一定偏角.
如图所示,一静电计与锌板相连,在A处用一紫外灯照射锌板,关灯后,指针保持一定偏角.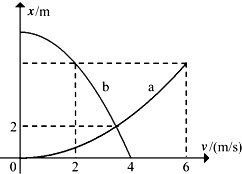 甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.质点甲做初速度为零,加速度大小为a1的匀加速直线运动.质点乙做初速度为v0,加速度大小为a2的匀减速直线运动至速度减为零后保持静止.甲、乙两质点在运动过程中的位置x-速度v图象如图所示,虚线与对应的坐标轴垂直.
甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.质点甲做初速度为零,加速度大小为a1的匀加速直线运动.质点乙做初速度为v0,加速度大小为a2的匀减速直线运动至速度减为零后保持静止.甲、乙两质点在运动过程中的位置x-速度v图象如图所示,虚线与对应的坐标轴垂直.  如图甲所示,固定在水平桌面上的光滑金属导轨cd、eg处于方向垂直导轨向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点C、e之间连接一电阻,其他部分电阻忽略不计.现用一水平向右的外力F1作用在金属杆ab上,使金属杆ab向右沿导轨滑动,滑动过程中金属杆ab始终垂直于导轨.金属杆ab受到的安培力用F2表示,F1与F2随时间t变化的关系图象如图乙所示,下面关于金属杆ab运动过程中的v-t图象不正确的是( )
如图甲所示,固定在水平桌面上的光滑金属导轨cd、eg处于方向垂直导轨向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点C、e之间连接一电阻,其他部分电阻忽略不计.现用一水平向右的外力F1作用在金属杆ab上,使金属杆ab向右沿导轨滑动,滑动过程中金属杆ab始终垂直于导轨.金属杆ab受到的安培力用F2表示,F1与F2随时间t变化的关系图象如图乙所示,下面关于金属杆ab运动过程中的v-t图象不正确的是( )