题目内容
6．
将三个质量均为m的小球a、b、c用细线相连后（bc间无细线相连），再用细线悬挂于O点，如图所示．用力F拉小球c，使三个小球都处于静止状态，且细线Oa与竖直方向的夹角保持为θ=30°，则F的最小值为（ ）| A． | mg | B． | 2mg | C． | 1.5mg | D． | $\frac{\sqrt{3}}{2}$mg |
分析 以三个小球组成的整体为研究对象，当F垂直于Oa线时取得最小值，根据平衡条件求解F的最小值
解答 解：静止时要将三球视为一个整体，重力为3mg，当作用于c球上的力F垂直于oa时，F最小，由正交分解法知：水平方向Fcos30°=Tsin30°，竖直方向Fsin30°+Tcos30°=3mg，解得Fmin=1.5mg．
故选：C
点评 这道题考查静力学平衡问题以及受力分析中的隔离法与整体法，本题使用的是整体法．
练习册系列答案
相关题目
16．下列说法中正确的是（ ）
| A． | 仅利用氧气的摩尔质量和阿伏加德罗常数这两个已知量，便可计算出氧气分子间的平均距离 | |
| B． | 对于一定质量的理想气体，温度升高，其压强的大小可能不变 | |
| C． | 固体很难被压缩是因为分子之间没有间隙 | |
| D． | 气体从外界吸收热量，气体的内能一定增大 |
17．
2011年11月1日我国成功发射了“神舟八号”卫星，如图是火箭点火升空瞬间时的照片，关于这一瞬间的火箭的速度和加速度的判断，下列说法正确的是（ ）
2011年11月1日我国成功发射了“神舟八号”卫星，如图是火箭点火升空瞬间时的照片，关于这一瞬间的火箭的速度和加速度的判断，下列说法正确的是（ ）| A． | 火箭的速度很小，但加速度可能较大 | |
| B． | 火箭的速度很大，加速度可能也很大 | |
| C． | 火箭的速度很小，所以加速度也很小 | |
| D． | 火箭的速度很大，但加速度一定很小 |
如图所示，一个大轮通过皮带拉着小轮转动，皮带和两轮之间无滑动，大轮的半径是小轮的2倍，大轮上的一点S离转动轴的距离是大轮半径的0.5倍，当大轮边缘上P点的向心加速度是10m/s2时，大轮上的S点和小轮上的Q点的向心加速度分别为aS=5m/s2，aQ=20m/s2．
1．
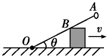如图所示，一根长为L的轻杆OA，O端用铰链固定，另一端固定着一个小球A，轻杆靠在一个高为h的物块上，物块与轻杆的接触点为B．若物块以速度v向右匀速运动，杆与水平方向夹角为θ，则下列说法正确的是（ ）
如图所示，一根长为L的轻杆OA，O端用铰链固定，另一端固定着一个小球A，轻杆靠在一个高为h的物块上，物块与轻杆的接触点为B．若物块以速度v向右匀速运动，杆与水平方向夹角为θ，则下列说法正确的是（ ）| A． | A、B的线速度相同 | B． | A、B的角速度不相同 | ||
| C． | 轻杆转动的角速度为$\frac{vLsi{n}^{2}θ}{h}$ | D． | 小球A的线速度大小为$\frac{vLsi{n}^{2}θ}{h}$ |
11．
在探究弹力和弹簧伸长量的关系时，某同学先按图1对弹簧甲进行探究，然后将弹簧乙和弹簧甲串联起来按图2进行探究．不考虑两个弹簧重力的影响，在弹性限度内，将质量m=50g的钩码逐个挂在弹簧下端，分别测得图1、图2中弹簧总长度L1、L2如表所示．
已知重力加速度g=9.8m/s2，要求尽可能多的利用测量数据，计算弹簧甲的劲度系数k=100N/m（保留三位有效数字）．由表中数据能（填“能”或“不能”）计算弹簧乙的原长．
在探究弹力和弹簧伸长量的关系时，某同学先按图1对弹簧甲进行探究，然后将弹簧乙和弹簧甲串联起来按图2进行探究．不考虑两个弹簧重力的影响，在弹性限度内，将质量m=50g的钩码逐个挂在弹簧下端，分别测得图1、图2中弹簧总长度L1、L2如表所示．| 钩码个数 | 1 | 2 | 3 | 4 |
| L1/cm | 26.00 | 26.48 | 26.97 | 27.47 |
| L2/cm | 79.44 | 80.89 | 82.36 | 83.85 |
如图所示，长L=1m的小车静止在光滑的水平面上，一滑块以v0=3m/s的水平
如图所示，直角棱镜ABC置于空气中，∠A=30°，AB边长为2a．一束单色光从D点垂直于BC边射入棱镜，在AC边上的E点恰好发生一次全反射后，从AB边中点F处射出．已知真空中光速为c．求：