题目内容
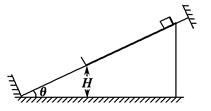
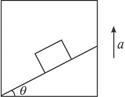
如图所示，一弹丸从离地高度H=1．95m的A点以v0=8．0m/s的初速度水平射出，恰以平行于斜面的速度射入静止在固定斜面顶端C处的一木块中，并立即与木块具有相同的速度（此速度大小为弹丸进入木块前一瞬间速度的
）共同运动，在斜面下端有一垂直于斜面的挡板，木块与它相碰没有机械能损失，碰后恰能返回C点。已知斜面顶端C处离地高h=0．15m，求
（1）A点和C点间的水平距离？
（2）木块与斜面间的动摩擦因数μ？
（3）木块从被弹丸击中到再次回到C点的时间t ？(保留两位有效数字，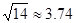
)
）共同运动，在斜面下端有一垂直于斜面的挡板，木块与它相碰没有机械能损失，碰后恰能返回C点。已知斜面顶端C处离地高h=0．15m，求（1）A点和C点间的水平距离？
（2）木块与斜面间的动摩擦因数μ？
（3）木块从被弹丸击中到再次回到C点的时间t ？(保留两位有效数字，
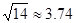)（1）4.8m（2）0．125（3）0．44s
（1）弹丸从A到C做平抛运动
t=
= 
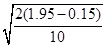s=0．6s
A点到C点的水平距离s = v0t =8．0×0．6m ="4.8m"
（2）弹丸到C的速度方向与水平方向的夹角为
tgθ =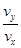
= 
= 
=
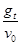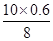vC=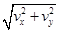
=
= 
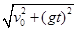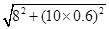m/s = 10m/s
弹丸与塑料块在C点具有的相同速度vC’=vC="1m/s"
分析弹丸与塑料块从C点返回到C点的整个过程，根据动能定理有：
-μmgcosθ×2×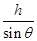
=0－
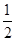mvC’2
解得动摩擦因数μ=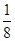
=0．125
（3）根据牛顿第二定律，下滑时由 a1=gsinθ-μgcosθ可得a1="5" m/s2
由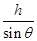= vC’ t1+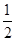a1 t12可解得t1=
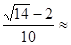0．17s
上滑时由 a1=gsinθ+μgcosθ可得a2="7" m/s2
由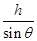=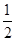a2t22可解得t2=
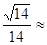0．27s
所以塑料块从被弹丸击中到再次回到C点的时间t= t1+ t2=0．44s
本题考查平抛运动动能定理的应用，根据平抛运动的竖直位移可求出运动时间，从而求出初速度，根据物体在斜面的运动应用动能定理求出动摩擦因数
t=
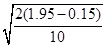= s=0．6sA点到C点的水平距离s = v0t =8．0×0．6m ="4.8m"
（2）弹丸到C的速度方向与水平方向的夹角为
tgθ =
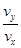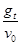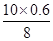= = =vC=
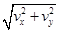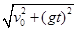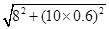== m/s = 10m/s弹丸与塑料块在C点具有的相同速度vC’=
vC="1m/s" 分析弹丸与塑料块从C点返回到C点的整个过程，根据动能定理有：
-μmgcosθ×2×
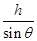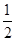=0－mvC’2 解得动摩擦因数μ=
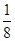=0．125 （3）根据牛顿第二定律，下滑时由 a1=gsinθ-μgcosθ可得a1="5" m/s2
由
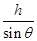= vC’ t1+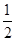a1 t12可解得t1=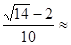0．17s上滑时由 a1=gsinθ+μgcosθ可得a2="7" m/s2
由
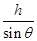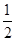=a2t22可解得t2=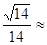0．27s 所以塑料块从被弹丸击中到再次回到C点的时间t= t1+ t2=0．44s
本题考查平抛运动动能定理的应用，根据平抛运动的竖直位移可求出运动时间，从而求出初速度，根据物体在斜面的运动应用动能定理求出动摩擦因数
练习册系列答案
名校课堂系列答案
相关题目
