题目内容
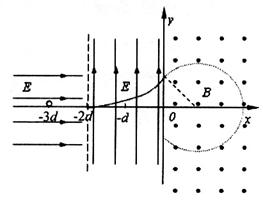
在xoy坐标平面内存在着如图所示的有理想边界的匀强电场和匀强磁场,在x<-2d的区域内匀强电场的场强为E、方向沿+x轴方向,在-2d<x<0的区域内匀强电场的场强为E、方向沿+y轴方向,在x>0的区域内匀强磁场的磁感应强度的大小为![]() ,方向垂直于该平面向外。一质量为m、带电荷量为+q的微粒从x轴上的x=-3d处由静止释放,经过-2d<x<0的匀强电场区域后进入匀强磁场。求:
,方向垂直于该平面向外。一质量为m、带电荷量为+q的微粒从x轴上的x=-3d处由静止释放,经过-2d<x<0的匀强电场区域后进入匀强磁场。求:
(1)微粒到达x=-2d处的速度;
(2)微粒离开电场时沿y轴正方向上的位移;
(3)微粒第一次打到x轴上的坐标。

解:(1)微粒在![]() 的区域内
的区域内
![]() ①(2分)
①(2分)
得微粒在![]() 处的速度
处的速度
![]() ②(1分)
②(1分)
(2)微粒在![]() 的区域内x轴方向上做匀速运动
的区域内x轴方向上做匀速运动
![]() ③(1分)
③(1分)
Y轴正方向上做初速度为零的匀加速直线运动
沿y轴正方向上的位移![]() ④(2分)
④(2分)
由②③④式可得Y=d ⑤(1分)
(3)经过y轴时,沿y轴正方向上的速度![]() ⑥(1分)
⑥(1分)
由②③⑤式可得![]() ⑦(1分)
⑦(1分)
微粒进入磁场时的速度![]() 方向与x轴成45°角 ⑧(1分)
方向与x轴成45°角 ⑧(1分)
微粒进入磁场后做匀速圆周运动
由![]() ⑨(2分)
⑨(2分)
得微粒做匀速圆周运动的半径R=![]() ⑩(1分)
⑩(1分)
其轨迹如图所示,由几何关系得微粒第一次打到x轴上的坐标是
![]() (1分)
(1分)

练习册系列答案
相关题目
 在xoy坐标平面内存在着如图所示的有理想边界的匀强电场和匀强磁场,在x<-2d的区域内匀强电场的场强为E、方向沿+x轴方向,在-2d<x<0的区域内匀强电场的场强为E、方向沿+y轴方向,在x>0的区域内匀强磁场的磁感应强度的大小为
在xoy坐标平面内存在着如图所示的有理想边界的匀强电场和匀强磁场,在x<-2d的区域内匀强电场的场强为E、方向沿+x轴方向,在-2d<x<0的区域内匀强电场的场强为E、方向沿+y轴方向,在x>0的区域内匀强磁场的磁感应强度的大小为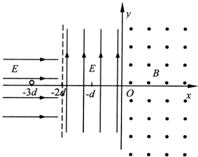

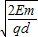 ,方向垂直于该平面向外.一质量为m、带电荷量为+q的微粒从x轴上的x=-3d处由静止释放,经过-2d<x<0的匀强电场区域后进入匀强磁场.求:
,方向垂直于该平面向外.一质量为m、带电荷量为+q的微粒从x轴上的x=-3d处由静止释放,经过-2d<x<0的匀强电场区域后进入匀强磁场.求: