题目内容
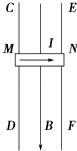
【题目】一电子（e，m）以速度v0与x轴成30°角垂直射入磁感强度为B的匀强磁场中，经一段时间后，打在x轴上的P点，如图所示，则P点到O点的距离为多少？电子由O点运动到P点所用的时间为多少？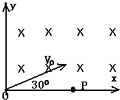
【答案】解：电子在磁场中受洛伦兹力作用做匀速圆周运动，轨迹如图所示：
由图可知：弦切角为30°，所以圆心角为60°
P点到O点的距离等于半径，
根据Bev0= 
得： 
所以P点到O点的距离等于 
圆周运动的周期 
圆心角为60°，所以电子由O点运动到P点所用的时间：t= 
答：则P点到O点的距离为 ，电子由O点运动到P点所用的时间为 
．
【解析】（1）先根据几何关系求出P点到O点的距离等于半径，再根据洛伦兹力提供向心力求出半径；（2）由几何关系得出运动的圆心角，再根据与周期的关系求出运动时间．
【考点精析】利用洛伦兹力和感应电流的方向对题目进行判断即可得到答案，需要熟知洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功；通电导体在磁场中受力方向：跟电流方向和磁感线方向有关．（左手定则）．
练习册系列答案
相关题目
