题目内容
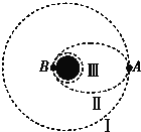
【题目】如图所示，一个内壁光滑的绝缘细直管竖直放置。在管子的底部固定一电荷量为Q（Q0） 的带电体，在距离底部点电荷为h2的管口A处，有一电荷量为q（q0）、质量为m的小球自静止释放，在距离底部点电荷为h1的B处速度恰好为零。现让一个电荷量为q、质量为2m的小球仍在A处自静止释放，已知静电力常量为k，重力加速度为g，则该小球
A. 运动到B处的速度为零
B. 在下落过程中加速度大小一直变小
C. 向下运动了位移
时速度最大
D. 小球向下运动到B点时的速度为
【答案】D
【解析】
A、B项：质量为m点电荷，从静止释放后开始下落，库仑力越来越大，所以点电荷先加速后减速。则加速度先减小后增大。当到达B点时，点电荷停止。由动能定理可得：
，得：
，而当换成质量2m点电荷时，仍从原来位置静止释放，则点电荷先加速后减速。则加速度先减小后增大，设停止的位置为B′，则由动能定理可得：
，所以
则速度为零的位置在B点下方，故AB错误；
C项：速度最大位置，就是加速度为零的位置。即库仑力与重力相等的位置，当质量为2m时，设平衡位置距底部点电荷的距离为h0′则有：
，所以
则向下运动的位移
，故C错误；
D项：点电荷从静止到B点，由动能定理可得：
，而所以B点时的速度为
，故D正确。
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
