题目内容
【题目】如图（甲）所示，蹦极是一项非常刺激的户外休闲活动。为了研究蹦极运动做以下简化：将跳跃者视为质量为m的质点，他的运动沿竖直方向，且初速度为0。弹性绳的原长为L，劲度系数为k，其形变量与所受拉力成正比。跳跃者下落1.5L时到达最低点。此过程中忽略空气阻力和弹性绳质量，重力加速度为g。求：
（1）当弹性绳刚好被拉直时，跳跃者的速度大小；
（2）当跳跃者速度达到最大时，距起跳平台的高度；
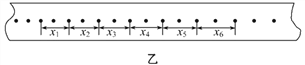
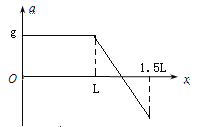
（3）取起跳位置为坐标原点O，取竖直向下为正方向，建立x轴。在跳跃者从开始跳下到最低点的过程中，跳跃者的位移为x，加速度为a，在图（乙）中定性画出a随x变化关系的图像。
【答案】（1）
（2）
（3）图见解析；
【解析】
（1）当弹性绳刚好被拉直时，跳跃者下落的竖直距离为L，根据v2=2gL
可得速度大小：v=；
（2）当跳跃者速度达到最大时，重力等于弹力，即mg=k(x-L)
解得此时距起跳平台的高度：
.
（3）从开始下落到弹性绳到达原长L的过程中，加速度为g不变；以后弹性绳被拉长，开始时弹力小于重力，加速度向下，且：
，随下降的高度增加，弹力逐渐变大，当弹力等于重力时加速度减为0；以后弹力大于重力，加速度向上变大，直到最低点，此时
，则a-x图像如图：
练习册系列答案
相关题目
