题目内容
 (2011?甘肃二模)如图所示,两物块A、B并排静置于高h=0.80m的光滑水平桌面上,物块的质量均为M=0.60kg.一颗质量m=0.10kg的子弹C以v0=100m/s的水平速度从左面射入A,子弹射穿A后接着射人B并留在B中,此时A、B都没有离开桌面.已知物块A的长度为0.27m,A离开桌面后,落地点到桌边的水平距离s=2.0m.设子弹在物块A、B中穿行时受到的阻力保持不变,g取l0m/s2.
(2011?甘肃二模)如图所示,两物块A、B并排静置于高h=0.80m的光滑水平桌面上,物块的质量均为M=0.60kg.一颗质量m=0.10kg的子弹C以v0=100m/s的水平速度从左面射入A,子弹射穿A后接着射人B并留在B中,此时A、B都没有离开桌面.已知物块A的长度为0.27m,A离开桌面后,落地点到桌边的水平距离s=2.0m.设子弹在物块A、B中穿行时受到的阻力保持不变,g取l0m/s2.(1)物块A和物块B离开桌面时速度的大小分别是多少;
(2)求子弹在物块B中穿行的距离;
(3)为了使子弹在物块B中穿行时物块B未离开桌面,求物块B到桌边的最小距离.
分析:(1)物块A做平抛运动,据此可求出A的速度大小,根据系统动量守恒可求出B与子弹的速度大小.
(2)根据子弹传木块过程中动量守恒以及功能关系列方程,可正确解答.
(3)子弹穿木块过程中分别以两木块为研究对象,根据动能定理列方程,即可求解.
(2)根据子弹传木块过程中动量守恒以及功能关系列方程,可正确解答.
(3)子弹穿木块过程中分别以两木块为研究对象,根据动能定理列方程,即可求解.
解答:解:(1)子弹射穿物块A后,A以速度vA沿桌面水平向右匀速运动,离开桌面后做平抛运动:
h=
gt2,解得:t=0.40s
A离开桌边的速度:vA=
,解得vA=5.0m/s. ①
设子弹射入物块B后,子弹与B的该题速度为vB,子弹与两物块作用过程系统动量守恒:
mv0=MvA+(M+m)vB ②
B离开桌边的速度vB=10m/s.
故物块A和物块B离开桌面时速度的大小分别是:vA=5.0m/s,vB=10m/s.
(2)设子弹离开A时的速度为v1,子弹与物块A作用过程系统动量守恒:
mv0=mv1+2MvA,解得:v1=40m/s.③
子弹在物块B中穿行的过程中,由能量守恒
fLB=
M
+
m
-
(M+m)
④
子弹在物块A中穿行的过程中,由能量守恒
fLA=
m
-
m
-
(M+M)
⑤
联立①⑤解得:LB=3.5×10-2m.
子弹在物块B中穿行的距离:LB=3.5×10-2m.
(3)子弹在物块A中穿行的过程中,物块A在水平桌面上的位移为s1,根据动能定理有:
fs1=
(M+m)
-0 ⑥
子弹在物块B中穿行的过程中,物块B在水平桌面上的位移s2,根据动能定理得:
fs2=
M
-
⑦
联立方程解得物块B到桌边的最小距离:Smin=s1+s2
ssim=2.5×10-2m.
故物块B到桌边的最小距离:Smin=s1+s2.
h=
| 1 |
| 2 |
A离开桌边的速度:vA=
| s |
| t |
设子弹射入物块B后,子弹与B的该题速度为vB,子弹与两物块作用过程系统动量守恒:
mv0=MvA+(M+m)vB ②
B离开桌边的速度vB=10m/s.
故物块A和物块B离开桌面时速度的大小分别是:vA=5.0m/s,vB=10m/s.
(2)设子弹离开A时的速度为v1,子弹与物块A作用过程系统动量守恒:
mv0=mv1+2MvA,解得:v1=40m/s.③
子弹在物块B中穿行的过程中,由能量守恒
fLB=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 B |
子弹在物块A中穿行的过程中,由能量守恒
fLA=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 A |
联立①⑤解得:LB=3.5×10-2m.
子弹在物块B中穿行的距离:LB=3.5×10-2m.
(3)子弹在物块A中穿行的过程中,物块A在水平桌面上的位移为s1,根据动能定理有:
fs1=
| 1 |
| 2 |
| v | 2 A |
子弹在物块B中穿行的过程中,物块B在水平桌面上的位移s2,根据动能定理得:
fs2=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| Mv | 2 A |
联立方程解得物块B到桌边的最小距离:Smin=s1+s2
ssim=2.5×10-2m.
故物块B到桌边的最小距离:Smin=s1+s2.
点评:利用功能关系和动量守恒解题时一定要选好状态,分析清楚运动过程,然后正确选择研究对象列方程求解,这类问题有一定难度,能够很好的考查学生综合分析问题的能力.

练习册系列答案
相关题目
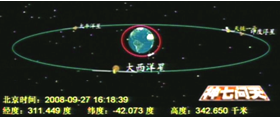 (2011?甘肃二模)2011我国计划发射“天宫一号”小型空间站,再发射神舟八号航天飞船与之对接;这与2008年9月我国成功发射神舟七号载人航天飞船类似.如图所示是神舟七号绕地球飞行时的电视直播画面,图中教据显示,飞船距地面的高度约为地球半径的
(2011?甘肃二模)2011我国计划发射“天宫一号”小型空间站,再发射神舟八号航天飞船与之对接;这与2008年9月我国成功发射神舟七号载人航天飞船类似.如图所示是神舟七号绕地球飞行时的电视直播画面,图中教据显示,飞船距地面的高度约为地球半径的 (2011?甘肃二模)水平放置的U形光滑金属导轨上放置一金属棒ab,甲图中的矩形区域内存在一有界匀强磁场,规定垂直纸面向里为磁场正方向.现使该磁场按乙图所示的规律变化,则下列判断正确的是( )
(2011?甘肃二模)水平放置的U形光滑金属导轨上放置一金属棒ab,甲图中的矩形区域内存在一有界匀强磁场,规定垂直纸面向里为磁场正方向.现使该磁场按乙图所示的规律变化,则下列判断正确的是( ) (2011?甘肃二模)如图所示,AD、BD、CD都是光滑的直角斜面,斜面固定在水平地面上,现使一小物体分别从A、B、C点由静止开始下滑到D点,所用时间分别为t1、t2、t3,则( )
(2011?甘肃二模)如图所示,AD、BD、CD都是光滑的直角斜面,斜面固定在水平地面上,现使一小物体分别从A、B、C点由静止开始下滑到D点,所用时间分别为t1、t2、t3,则( )