题目内容
如图所示，用长L=0.50m的绝缘轻质细线，把一个质量m=1.0g带电小球悬挂在带等量异种电荷的平行金属板之间，平行金属板间的距离d=5.0cm，两板间电压U=1.0×103V．静止时，绝缘线偏离竖直方向θ角，小球偏离竖直距离a=1.0cm．（θ角很小，为计算方便可认为tanθ≈sinθ，取g=10m/s2，需要求出具体数值，不能用θ角表示），则
（1）两板间电场强度的大小为
2.0×104
2.0×104
V/m；（2）小球带的电荷量
1.0×10-8C
1.0×10-8C
C（3）若细线突然被剪断，小球将在板间
匀加速直线运动
匀加速直线运动
（填“类平抛运动”、“匀加速直线运动”或“匀速直线运动”）分析：由电场强度与电势差的关系，可求电场强度；对小球受力分析，有平衡条件求电场力，求电荷量；细线断后小球受到重力、电场力，合力为恒力，做匀加速直线运动．
解答：解：（1）由电场强度与电势差的关系，得E=
=
=2.0×104V/m；
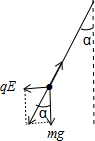
（2）对小球受力分析如图，则qE=mgtanα q=
=
=1.0×10-8C
（3）由受力图知，当细线断后小球受到重力、电场力作用，合力为恒力，有牛顿第二定律得，加速度恒定，故做匀加速直线运动
故答案为：（1）两板间电场强度的大小为 2.0×104 V/m；
（2）小球带的电荷量 1.0×10-8CC
（3）若细线突然被剪断，小球将在板间 匀加速直线运动．
| u |
| d |
| 1.0×103 |
| 0.05 |
（2）对小球受力分析如图，则qE=mgtanα q=
| mgtanα |
| E |
1.0×10-3×10×
| ||
| 2.0×104 |
（3）由受力图知，当细线断后小球受到重力、电场力作用，合力为恒力，有牛顿第二定律得，加速度恒定，故做匀加速直线运动
故答案为：（1）两板间电场强度的大小为 2.0×104 V/m；
（2）小球带的电荷量 1.0×10-8CC
（3）若细线突然被剪断，小球将在板间 匀加速直线运动．
点评：考查了带电粒子在电场中的受力平衡问题，由受力情况，判断运动情况．
练习册系列答案
相关题目
如图所示，用长L=0.50m的绝缘轻质细线，把一个质量m=1.0g带电小球悬挂在带等量异种电荷的平行金属板之间，平行金属板间的距离d=5.0cm，两板间电压U=1.0×103V．静止时，绝缘线偏离竖直方向θ角，小球偏离竖直距离a=1.0cm．（θ角很小，为计算方便可认为tanθ≈sinθ，取g=10m/s2，需要求出具体数值，不能用θ角表示）求：
