题目内容
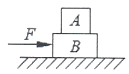
【题目】将一轻弹簧竖直放置在地面上,在其顶端由静止释放一质量为m的物体,当弹簧被压缩到最短时,其压缩量为l。现将该弹簧的两端分别栓接小物块A与B,并将它们静置于倾角为30°的足够长固定斜面上,B靠在垂直于斜面的挡板上,P点为斜面上弹簧自然状态时A的位置,如图所示。由斜面上距P点6l的O点,将另一物块C以初速度t=5![]() 沿斜面向下滑行,经过一段时间后与A发生正碰,碰撞时间极短,碰后C、A紧贴在一起运动,但不粘连,已知斜面P点下方光滑、上方粗糙,A、B、C的质量均为4m,与斜面间的动摩擦因数均为μ=
沿斜面向下滑行,经过一段时间后与A发生正碰,碰撞时间极短,碰后C、A紧贴在一起运动,但不粘连,已知斜面P点下方光滑、上方粗糙,A、B、C的质量均为4m,与斜面间的动摩擦因数均为μ=![]() ,弹簧劲度系数k=
,弹簧劲度系数k=![]() ,弹簧始终在弹性限度内,重力加速度为g。求:
,弹簧始终在弹性限度内,重力加速度为g。求:
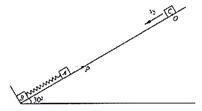
(1)C与A碰撞前瞬间的速度大小;
(2)C最终停止的位置与O点的距离
(3)判断上述过程中B能否脱离挡板,并说明理由。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]() ,说明此时A仍有沿斜面向上速度,故B可以离开挡板
,说明此时A仍有沿斜面向上速度,故B可以离开挡板
【解析】
(1)刚开始A压缩弹簧,设此时弹簧压缩量为![]() ,对A根据平衡条件可得
,对A根据平衡条件可得![]()
解得![]()
设C与A碰前瞬间速度大小为![]() ,由动能定理得:
,由动能定理得:
![]()
由以上式子得:![]()
(2)依题意,当竖直放置的弹簧被压缩l时,质量为m的物体的动能为零,其重力势能转化为弹簧的弹性势能,由机械能守恒定律,弹簧的弹性势能为:![]()
C与A碰撞过程中动量守恒,有![]()
C与A后返回P点过程,B始终未动,对A、C及弹簧组成的系统,根据机械能守恒定律得:![]()
此后C与A分离,C沿斜面向上做匀减速运动直至停下,根据动能定理可得:
![]()
由以上式子得![]() ,即C最终停止的位置与O点相距4l
,即C最终停止的位置与O点相距4l
(3)要使B离开挡板,则弹簧必须伸长到![]() ,即A需到达斜面上P点上方l处,此时弹簧弹性势能恰也为
,即A需到达斜面上P点上方l处,此时弹簧弹性势能恰也为![]()
假定A可以到达该处,即对A由P至该处的运动过程,根据动能定理得:
![]()
其中![]()
由以上式子可得![]() ,说明此时A仍有沿斜面向上的速度,故B可以离开挡板。
,说明此时A仍有沿斜面向上的速度,故B可以离开挡板。

练习册系列答案
相关题目