题目内容
 如图所示,竖直平行直线为匀强电场的电场线,电场方向未知,AB是电场中的两点,AB两点的连线长为l,且与电场线所夹锐角为θ,一个质量为m电量为-q的带电粒子以初速度V0从A点垂直于电场方向射入电场,该带电粒子恰好能经过B点,不考虑带电粒子的重力大小.
如图所示,竖直平行直线为匀强电场的电场线,电场方向未知,AB是电场中的两点,AB两点的连线长为l,且与电场线所夹锐角为θ,一个质量为m电量为-q的带电粒子以初速度V0从A点垂直于电场方向射入电场,该带电粒子恰好能经过B点,不考虑带电粒子的重力大小.(1)根据你学过的物理学规律和题中所给的信息,对反映电场本身性质的物理量(例如电场方向),你能得出哪些定性判断或求得哪些定量结果.
(2)若仅知道带电小球的电量-q、初动能EK0以及AB两点的连线与电场线所夹锐角θ三个量,以A点为零电势点,则点电荷经过B点时的电势能是多少?
分析:(1)粒子在电场中做类平抛运动,结合带电粒子在水平方向和竖直方向上的运动规律求出AB两点的电场强度,以及根据匀强电场的电势差的公式求出A、B两点的电势差.通过粒子的电性判断电场强度的方向,从而确定A、B两点电势的高低.
(2)设初速度大小为v0,小球过B点竖直分速度为vy,瞬时速度为vB,水平和竖直位移分别为x和y,根据运动学基本公式、动能定理即可求解AB两点的电势差,进而求出B点电势,从而求出电势能.
(2)设初速度大小为v0,小球过B点竖直分速度为vy,瞬时速度为vB,水平和竖直位移分别为x和y,根据运动学基本公式、动能定理即可求解AB两点的电势差,进而求出B点电势,从而求出电势能.
解答:解:(1)因粒子带负电且向下偏转,故电场力方向向下,所以电场方向竖直向上.
水平方向匀速运动,有:lsinθ=v0t
竖直方向做初速度为零的匀加速运动,有
lcosθ=
at2
则加速度a=
由qE=ma,得电场强度大小:E=
=
B点的电势高于A点的电势,有A、B两点间的电势差为:
UAB=-Elcosθ=-
(2)设初速度大小为v0,小球过B点竖直分速度为vy,瞬时速度为vB,
水平和竖直位移分别为x和y,则有:y=
t,x=v0t
而
=cotθ
所以vy=2v0cotθ
由动能定理得:-qUAB=
mvB2-
mv02=
mvy2
所以A、B间的电势差UAB=-
以A点为零电势点,则B点的电势为:φB=
所以点电荷经过B点时的电势能为E=φBq=4Ek0(cotθ)2
答:(1)电场强度大小为
,电场方向竖直向上,A、B两点间的电势差为-
;
(2)点电荷经过B点时的电势能是4Ek0(cotθ)2.
水平方向匀速运动,有:lsinθ=v0t
竖直方向做初速度为零的匀加速运动,有
lcosθ=
| 1 |
| 2 |
则加速度a=
| 2v02cosθ |
| l(sinθ)2 |
由qE=ma,得电场强度大小:E=
| ma |
| q |
| 2mv02cosθ |
| ql(sinθ)2 |
B点的电势高于A点的电势,有A、B两点间的电势差为:
UAB=-Elcosθ=-
| 2mv02(cosθ)2 |
| q(sinθ)2 |
(2)设初速度大小为v0,小球过B点竖直分速度为vy,瞬时速度为vB,
水平和竖直位移分别为x和y,则有:y=
| vy |
| 2 |
而
| y |
| x |
所以vy=2v0cotθ
由动能定理得:-qUAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以A、B间的电势差UAB=-
| 4Ek0(cotθ)2 |
| q |
以A点为零电势点,则B点的电势为:φB=
| 4Ek0(cotθ)2 |
| q |
所以点电荷经过B点时的电势能为E=φBq=4Ek0(cotθ)2
答:(1)电场强度大小为
| 2mv02cosθ |
| ql(sinθ)2 |
| 2v02(cosθ)2 |
| q(sinθ)2 |
(2)点电荷经过B点时的电势能是4Ek0(cotθ)2.
点评:本题是道开放题,关键抓住粒子的运动规律并能结合几何关系进行求解,难度较大.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目

 =45°的位置;若平行板以M、N为轴同时顺时针旋转
=45°的位置;若平行板以M、N为轴同时顺时针旋转 =15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
=15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
 变为
变为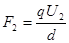 ,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。
,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。 =45°的位置;若平行板以M、N为轴同时顺时针旋转
=45°的位置;若平行板以M、N为轴同时顺时针旋转 =15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
=15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
 变为
变为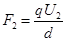 ,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。
,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。 =45°的位置;若平行板以M、N为轴同时顺时针旋转
=45°的位置;若平行板以M、N为轴同时顺时针旋转 =15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
=15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
 变为
变为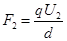 ,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。
,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。 =45°的位置;若平行板以M、N为轴同时顺时针旋转
=45°的位置;若平行板以M、N为轴同时顺时针旋转 =15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
=15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
 变为
变为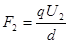 ,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。
,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。