题目内容
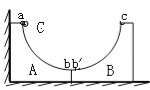
【题目】如图所示，半径均为R，质量均为M，内表面光滑的两个完全相同的1/4圆槽A、B并排放在光滑的水平面上，图中a、c分别为A、B槽的最高点，b、b/分别为A、B槽的最低点，A槽的左端紧靠着墙壁，一个质量为m的小球C从圆槽的顶端的a点无初速释放，求：
（1）小球C从a点运动到b点时的速度及A槽对地面的压力；
（2）小球C在B槽内运动所能到达最大高度；
（3）B的最大速度是多少？
【答案】（1）3mg+Mg；（2）
；（3）
【解析】
试题分析：（1）由a到b由机械能守恒定律可得：
，解得
在最低点b，根据牛顿第二定律可得：
，解得N=3mg
根据牛顿第三定律可知A槽对地面的压力为3mg+Mg.
（2）小球到达B球的最高点时，两者共速，由动量守恒定律可知：mv0=(M+m)v
由能量关系可知：
解得：
（3）当小球回到槽的底端时，槽B的速度最大，此时根据动量守恒定律：
由能量守恒关系可知：
解得：
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
