题目内容
5. 如图所示,质量m=1kg的物块A放在质量M=4kg木板B的左端,起初A、B静止在光滑水平地面上,现用一水平向左的力F作用在木板B上,已知AB之间的动摩擦因数为μ=0.4,假设最大静摩擦力等于滑动摩擦力,g=10m/s2.求:
如图所示,质量m=1kg的物块A放在质量M=4kg木板B的左端,起初A、B静止在光滑水平地面上,现用一水平向左的力F作用在木板B上,已知AB之间的动摩擦因数为μ=0.4,假设最大静摩擦力等于滑动摩擦力,g=10m/s2.求:(1)能使AB发生相对滑动的F的最小值;
(2)若F=24N,作用1s后撤去,要想A不从B上滑落,则木板至少多长?
分析 (1)当AB保持相对静止时,两者具有相同的加速度,当A、B间的摩擦力达到最大静摩擦力,分别对A和整体利用牛顿第二定律求出F的最小值.
(2)根据牛顿第二定律,运用整体法和隔离法判断撤去拉力后,A、B能否保持相对静止,再分别对A、B运用牛顿第二定律和运动学公式,求出A不从B上滑落时木板至少的长度以及从开始到AB均静止A的总位移.
解答 解:(1)当AB保持相对静止时,两者具有相同的加速度,当A、B间的摩擦力达到最大静摩擦力,对于A,由牛顿第二定律得:
μmg=am
代入数据解得:am=4m/s2.
对AB整体,由牛顿第二定律得:
Fmin=(M+m)am
代入数据解得:Fmin=20N
(2)设F作用在B上时,A、B的加速度分别为a1、a2,撤去F时速度分别为v1、v2,撤去外力F后加速度分别为a1′、a2′.AB共同运动时速度为v3,加速度为a2,AB都做匀加速直线运动.
对A,由牛顿第二定律可得:μmg=ma1
代入数据解得:a1=4m/s2.
由速度公式得:v1=a1t1=4×1=4m/s
对B,由牛顿第二定律得:F-μmg=Ma2
代入数据解得:a2=5m/s2.
由速度公式得:v2=a2t1=5×1=5m/s
撤去外力后:a1′=a1=4m/s2,a2′=$\frac{μmg}{M}$=$\frac{0.4×1×10}{4}$=1m/s2.
经过t2时间后AB速度相等,有:v1+a1′t2=v2-a2′t2.
代入数据解得:t2=0.2s
则共同速度为:v3=v1+a1′t2=4+4×0.2=4.8m/s
从开始到AB相对静止.AB的相对位移即为木板最短的长度L
L=xB-xA=$\frac{{v}_{2}^{2}}{2{a}_{2}}$+$\frac{{v}_{2}^{2}-{v}_{3}^{2}}{2{a}_{2}′}$-$\frac{1}{2}$a1(t1+t2)2
代入数据解得 L=0.6 m
答:(1)能使AB发生相对滑动的F的最小值为20N.
(2)木板长至少为0.6m.
点评 本题属于牛顿运动定律中的典型模型“板块模型”,可以结合牛顿第二定律和运动学公式综合求解,.解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解,注意物体和木板相对滑动到相对静止的临界状态和整体法、隔离法的运用.


| A. | 通过电阻R的电流是交变电流 | B. | 感应电流的大小保持不变 | ||
| C. | 电阻R两端的电压为6V | D. | C点的电势为6V |
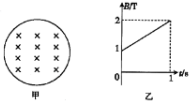 如图甲所示,面积为S=1m2的导体圆环内通有垂直于圆平面向里的磁场,磁场的磁感应强度B随时间t变化的关系如图乙所所示(B取向里方向为正),以下说法中正确的是( )
如图甲所示,面积为S=1m2的导体圆环内通有垂直于圆平面向里的磁场,磁场的磁感应强度B随时间t变化的关系如图乙所所示(B取向里方向为正),以下说法中正确的是( )| A. | 环中产生顺时针方向的感应电流 | B. | 环中产生逆时针方向的感应电流 | ||
| C. | 环中产生的感应电动势大小为2V | D. | 环中产生的感应电动势大小为1V |
| A. | 在一定拉力作用下,车沿水平方向前进,所以力是维持物体运动的原因 | |
| B. | 车原来静止,在水平向右推力作用下加速运动,说明力是改变物体运动状态的原因 | |
| C. | 质量小的物体运动状态容易改变是由于物体的质量小,惯性也就小的缘故 | |
| D. | 高速行驶的汽车由于速度大,所以惯性大,很难停下来 |
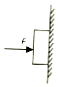
| A. | 竖直向上 | B. | 竖直向下 | C. | 水平向左 | D. | 水平向右 |
| A. | 牛顿不仅提出了万有引力定律而且测量出了引力常量 | |
| B. | 库仑在发现电荷间相互作用力规律之前,首先找到了定量测定电荷量的方法 | |
| C. | 库仑利用库仑扭秤巧妙地实现了他对电荷间相互作用力规律的研究 | |
| D. | 在国际单位中,力学的基本单位是米、牛顿、秒 |