Question

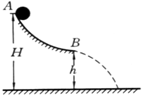
小球自高为H的A点由静止开始沿光滑曲面下滑，到曲面底处B飞离曲面，B处曲面的切线沿水平方向，B的高度h=H/2，若其他条件不变，只改变h，则小球的水平射程s的变化情况为（　　）

A．h增大时，s也增大	B．h增大时，s减小
C．h减小时，s也减小	D．h减小时，s增大

Answer 1

小球在曲面上的时候，小球的机械能守恒，根据机械能守恒可得，
mg（H-h）=

1

2

mv²，
所以小球到达B点时的速度的大小为，v=

2g(H-h)

小球离开B之后做的是平抛运动，
小球的运动的时间为t，
则 h=

1

2

gt²，
所以小球的运动的时间为t=

2h g

小球在水平方向上的射程为，
x=vt=

2g(H-h)

×

2h g

根据二次函数的极值问题得
当H-h=h时有最大值，即B的原来的高度h=

H

2

时，有最大值，所以无论h增大还是减小，s都减小．所以AD错误，BC正确；
故选BC