题目内容
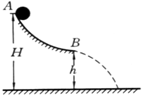
 小球自高为H的A点由静止开始沿光滑曲面下滑,到曲面底处B飞离曲面,B处曲面的切线沿水平方向,B的高度h=H/2,若其他条件不变,只改变h,则小球的水平射程s的变化情况为( )
小球自高为H的A点由静止开始沿光滑曲面下滑,到曲面底处B飞离曲面,B处曲面的切线沿水平方向,B的高度h=H/2,若其他条件不变,只改变h,则小球的水平射程s的变化情况为( )分析:小球做的是平抛运动,平抛运动可以分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动,物体运动的时间是由竖直下落的高度决定的,再由水平方向上的匀速直线运动找出水平射程s的表达式,根据表达式来分析水平射程的变化.
解答:解:小球在曲面上的时候,小球的机械能守恒,根据机械能守恒可得,
mg(H-h)=
mv2,
所以小球到达B点时的速度的大小为,v=
小球离开B之后做的是平抛运动,
小球的运动的时间为t,
则 h=
gt2,
所以小球的运动的时间为t=
小球在水平方向上的射程为,
x=vt=
×
根据二次函数的极值问题得
当H-h=h时有最大值,即B的原来的高度h=
时,有最大值,所以无论h增大还是减小,s都减小.所以AD错误,BC正确;
故选BC
mg(H-h)=
| 1 |
| 2 |
所以小球到达B点时的速度的大小为,v=
| 2g(H-h) |
小球离开B之后做的是平抛运动,
小球的运动的时间为t,
则 h=
| 1 |
| 2 |
所以小球的运动的时间为t=
|
小球在水平方向上的射程为,
x=vt=
| 2g(H-h) |
|
根据二次函数的极值问题得
当H-h=h时有最大值,即B的原来的高度h=
| H |
| 2 |
故选BC
点评:本题是考查学生对平抛运动规律的应用,在分析本题的时候,由于小球做平抛运动的高度h是变化的,所以小球在水平方向上的位移也是变化,所以解决本题的关键是找出水平位移的变化关系式,根据关系式即可分析水平的位移的变化的情况.

练习册系列答案
相关题目
 如图所示,小球自高为H的A点由静止开始沿光滑曲面下滑,到曲面底B点飞离曲面,B点处曲面的切线沿水平方向.若其他条件不变,只改变h,则小球的水平射程s的变化情况是( )
如图所示,小球自高为H的A点由静止开始沿光滑曲面下滑,到曲面底B点飞离曲面,B点处曲面的切线沿水平方向.若其他条件不变,只改变h,则小球的水平射程s的变化情况是( )