题目内容
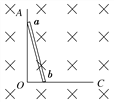
【题目】如图所示，矩形区域abcdef分为两个矩形区域，左侧区域充满匀强电场，方向竖直向上，右侧区域充满匀强磁场，方向垂直纸面向外，be为其分界线，af＝L，ab＝0.75L，bc＝L。一质量为m、电荷量为e的电子（重力不计）从a点沿ab方向以初速度v0射入电场，从be边的中点g进入磁场。（已知sin37°＝0.6，cos37°＝0.8）
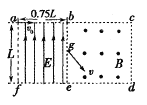
（1）求匀强电场的电场强度E的大小；
（2）若要求电子从cd边射出，求所加匀强磁场磁感应强度的最大值Bm；
（3）调节磁感应强度的大小．求cd边上有电子射出部分的长度。
【答案】（1）
（2） 
（3）
【解析】试题分析：电子在电场中做类平抛运动，根据类平抛运动的规律和牛顿第二定律列式求解；电子在磁场中做匀速圆周运动，画出运动轨迹图，根据几何知识求匀强磁场磁感应强度的最大值；先根据运动的分解求出粒子进入磁场时的速度，画出两条临界轨迹如图，电子刚好不从cd边射出的半径为r1，电子刚好从de边射出时半径为r2，根据几何知识分别求出半径r1和r2，再根据几何关系求出cd边上有电子射出部分的长度。
（1）电子在电场中做类似平抛运动，有
在竖直方向： 
水平方向：0.75L＝v0t
由牛顿第二定律有：eE＝ma
联立解得： 
（2）粒子进入磁场时，速度方向与be边夹角的正切值tanθ＝
＝0.75，解得：θ＝37°
电子进入磁场时的速度为
设电子运动轨迹刚好与cd边相切时，半径最小为r1，轨迹如图所示：
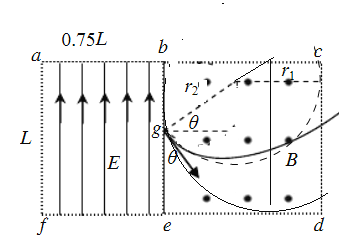
则由几何关系知r1＋r1cos37°＝L
解得： 
由洛伦兹力提供向心力： 
可得对应的最大磁感应强度： 
（3）设电子运动轨迹刚好与de边相切时，半径为r2，
则
解得： 
又r2cosθ＝L，故切点刚好为d点
电子从cd边射出的长度为： 
练习册系列答案
相关题目
