Question

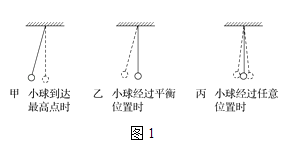
【题目】如图所示，让摆球从图中的A位置由静止开始下摆，正好摆到最低点B位置时线被拉断．设摆线长l=1.6m，悬点到地面的竖直高度为H=6.6m，不计空气阻力，求：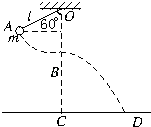

（1）摆球落地时的速度的大小．
（2）落地点D到C点的距离（g=10m/s2）．

Answer 1

【答案】
（1）解；小球从A运动到B的过程中受重力和线的拉力，只有重力做功；球从B到D做平抛运动，也只有重力做功，故小球从A点到D的全过程中机械能守恒．

取地面为参考平面．则得：

mg（H﹣lcos60°）= mvD2

得：vD= = =10.8m/s

答：摆球落地时的速度的大小是10.8m/s．

（2）解；小球从A到B的过程中，根据机械能守恒定律得：

mgl（1﹣cos60°）=

得：vB= = =4m/s

小球从B点开始做平抛运动，由平抛运动的规律，在竖直方向上有：

H﹣l= ，

得：t= = s=1s；

水平方向上，落地点D到C点的距离为：

x=vBt=4×1m=4m

答：落地点D到C点的距离是4m．

【解析】（1）小球沿圆弧下落的过程中和平抛运动过程中都满足机械能守恒根据机械能守恒列式求解。
（2）先求小球到达B点时的速度再根据平抛运动的规律进行求解。
【考点精析】关于本题考查的平抛运动和机械能守恒及其条件，需要了解特点:①具有水平方向的初速度;②只受重力作用，是加速度为重力加速度g的匀变速曲线运动；运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动；在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变才能得出正确答案．