题目内容
【题目】如图，半径R=1.0m的光滑圆弧轨道ABC与足够长的粗糙轨道CD在C处平滑连接，O为圆弧轨道ABC的圆心，B点为圆弧轨道的最低点，半径OA、OC与OB的夹角分别为53°和37°，将一个质量m=1.0kg的物体（视为质点）从A点左侧高为h=0.8m处的P点水平抛出，恰从A点沿切线方向进入圆弧轨道，已知物体与轨道CD间的动摩擦因数μ=0.5，重力加速度
，sin37°=0.6，cos37°=0.8，求：
（1）物体水平抛出时的初速度大小
；
（2）物体经过B点时受圆弧轨道支持力大小
；
（3）物体在轨道CD上向上运动的最大距离x。
【答案】（1）
（2）3N（3）
【解析】
（1）物体做平抛运动，由自由落体运动的规律求出物体落在A时的竖直分速度，然后应用运动的合成与分解求出物体的初速度大小v0．
（2）通过计算分析清楚物体的运动过程，由能量守恒定律求出物体在B点的速度，然后又牛顿第二定律求出物体对圆弧轨道压力大小FN；
（3）先由机械能守恒求出物体在C点的速度，然后由动能定理即可求解．
（1）物体在抛出后竖直方向做自由落体运动，竖直方向：
物体恰从A点沿切线方向进入圆弧轨道，则：
＝tan53°
得：
（2）物体到达A点的速度：
A到B的过程中机械能守恒，得：
mv2+mgR(1cos53°)＝mvB2
物体在B点受到的支持力与重力的合力提供向心力，则：FNmg＝
得：FN=3N；
（3）B到C的过程中机械能守恒，得：mvC2+mgR(1cos37°)＝mvB2
得：vC＝
m/s
物体在斜面CD上受到的摩擦力：f=μmgcos37°=0.5×1.0×10×0.8N=4N
设物体在轨道CD上运动的距离x，则：fxmgxsin37°＝0mvC2
解得：x=1.45m；
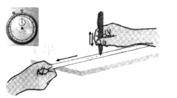
【题目】（1）如图所示，你的左手拿一块表，右手拿一支彩色画笔。你的同伴牵动一条宽约1 cm的长纸带，使纸带在你的笔下沿着直线向前移动。每隔1s你用画笔在纸带上点一个点。你还可以练习在1s内均匀地点上两个点。这样，就做成了一台简单的“打点计时器”。由实验可知纸带速度越大，相邻两点的距离越___________，纸带的速度与相邻两点所表示的时间__________（填“有”或“没有”）影响。
（2）小张以同一个打点计时器在固定频率下，測量小车拉动纸带甲、乙、丙、丁的运动速度，每次车子都是自右向左运动，四段纸带的长度都相同。如图，则下列叙述正确是
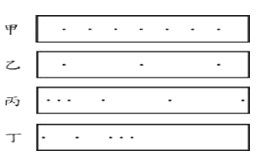
A．纸带甲打点均匀，表示车子的运动是匀速的，加速度是零。 |
B．纸带乙显示的平均速度与纸带甲相同 |
C．纸带丙表示的小车的运动是先快后慢 |
D．纸带丁表示的小车的运动是先慢后快 |
