题目内容
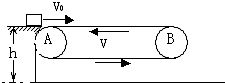如图所示，一长L=8m的水平传送带AB以V=2m/s的速度逆时针匀速转动，现一小物块以V0=6m/s的速度从传送带左侧AB滑上传送带，已知物块与带面间的动摩擦因数为0.2，物体距离地面的高度h=0.4m．（g取10m/s2）求：（1）物块达B点时速度多大？
（2）物块落地的水平位移？
（3）物块落地时速度方向如何？（用与 竖直方向的正切值表示）
分析：（1）根据牛顿第二定律结合运动学公式求出物块到达B点的速度大小．
（2）物块离开传送带做平抛运动，根据高度求出平抛运动的时间，根据初速度和时间求出水平位移．
（3）结合平抛运动水平方向和竖直方向上的运动规律求出物块落地时的速度方向．
（2）物块离开传送带做平抛运动，根据高度求出平抛运动的时间，根据初速度和时间求出水平位移．
（3）结合平抛运动水平方向和竖直方向上的运动规律求出物块落地时的速度方向．
解答：解：（1）根据牛顿第二定律得，a=
=μg=2m/s2
根据匀变速直线运动的位移时间公式得，L=v0t-
at2
代入数据8=6t-t2解得：t1=2s t1=4s（舍去，因为物块速度减为零所需的时间为3s）
vB=v0-at=6-2×2=2m/s．
（2）平抛运动的时间t=
=0.4s
水平位移 x=vBt=0.8m
（3）设速度与竖直方向的夹角为θ，
tanθ=
=
=
．
答：（1）物块达B点时速度为2m/s．
（2）物块落地的水平位移为0.8m．
（3）物块落地时速度方向与竖直方向的正切值为
．
| f |
| m |
根据匀变速直线运动的位移时间公式得，L=v0t-
| 1 |
| 2 |
代入数据8=6t-t2解得：t1=2s t1=4s（舍去，因为物块速度减为零所需的时间为3s）
vB=v0-at=6-2×2=2m/s．
（2）平抛运动的时间t=
|
水平位移 x=vBt=0.8m
（3）设速度与竖直方向的夹角为θ，
tanθ=
| vx |
| vy |
| vB |
| gt |
| 1 |
| 2 |
答：（1）物块达B点时速度为2m/s．
（2）物块落地的水平位移为0.8m．
（3）物块落地时速度方向与竖直方向的正切值为
| 1 |
| 2 |
点评：解决本题的关键知道物块在传送带上做匀减速直线运动，然后做平抛运动，结合牛顿第二定律和运动学公式进行求解．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
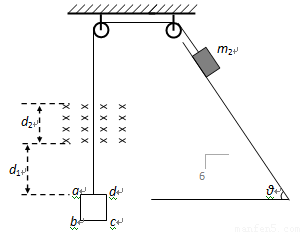
如图所示，一边长L=0.2m，质量m1=0.5kg，电阻R=0.1Ω的正方形导体线框abcd，与一质量为m2=2kg的物块通过轻质细线跨过两定滑轮相连．起初ad边距磁场下边界为d1=0.8m，磁感应强度B=2.5T，磁场宽度d2=0.3m，物块放在倾角θ=53°的斜面上，物块与斜面间的动摩擦因数μ=0.5．现将物块由静止释放，经一段时间后发现当ad边从磁场上边缘穿出时，线框恰好做匀速运动．（g取10m/s，sin53°=0.8，cos53°=0.6）求：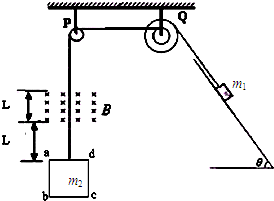
如图所示，一边长L，质量m2=m，电阻为R的正方形导体线框abcd，与一质量为m1=2m的物块通过轻质细线绕过定滑轮P和轮轴Q后相联系，Q的轮和轴的半径之比为r1：r2=2：1．起初ad边距磁场下边界为L，磁感应强度B，磁场宽度也为L，且物块放在倾角θ=53°的斜面上，斜面足够长，物块与斜面间的动摩擦因数μ=0.5．现将物块由静止释放，经一段时间后发现当ad边从磁场上边缘穿出时，线框恰好做匀速运动．（sin53°=0.8，cos53°=0.6）求：
=37°角，以
沿逆时针方向匀速传动，一质量为M=0.5kg的物块在传送带的顶端由静止释放，物块与传送带间的动摩擦因数为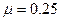
，当物块滑到底端时，有一质量为m=0.01kg的子弹以
原速度射入物块，后又以
的速度穿出物块，以后每隔
就有相同的子弹以相同的速度射入和穿出。（不计子弹穿过物块的时间，sin37°=0.6,cos37=0.8）
=37°角，以
沿逆时针方向匀速传动，一质量为M=0.5kg的物块在传送带的顶端由静止释放，物块与传送带间的动摩擦因数为
，当物块滑到底端时，有一质量为m=0.01kg的子弹以
原速度射入物块，后又以
的速度穿出物块，以后每隔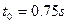
就有相同的子弹以相同的速度射入和穿出。（不计子弹穿过物块的时间，sin37°=0.6,cos37=0.8）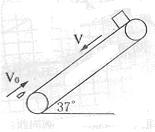
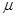=0.5。现将物块由静止释放，经一段时间后发现当ad边从磁场上边缘穿出时，线框恰好做匀速运动。（g取10m/s2，sin530=0.8，cos530=0.6）求：