题目内容
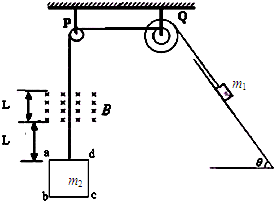 如图所示,一边长L,质量m2=m,电阻为R的正方形导体线框abcd,与一质量为m1=2m的物块通过轻质细线绕过定滑轮P和轮轴Q后相联系,Q的轮和轴的半径之比为r1:r2=2:1.起初ad边距磁场下边界为L,磁感应强度B,磁场宽度也为L,且物块放在倾角θ=53°的斜面上,斜面足够长,物块与斜面间的动摩擦因数μ=0.5.现将物块由静止释放,经一段时间后发现当ad边从磁场上边缘穿出时,线框恰好做匀速运动.(sin53°=0.8,cos53°=0.6)求:
如图所示,一边长L,质量m2=m,电阻为R的正方形导体线框abcd,与一质量为m1=2m的物块通过轻质细线绕过定滑轮P和轮轴Q后相联系,Q的轮和轴的半径之比为r1:r2=2:1.起初ad边距磁场下边界为L,磁感应强度B,磁场宽度也为L,且物块放在倾角θ=53°的斜面上,斜面足够长,物块与斜面间的动摩擦因数μ=0.5.现将物块由静止释放,经一段时间后发现当ad边从磁场上边缘穿出时,线框恰好做匀速运动.(sin53°=0.8,cos53°=0.6)求:(1)线框与物体在任一时刻的动能之比;
(2)ad边从磁场上边缘穿出时速度的大小;
(3)ad刚进入磁场时线框动能的大小和线框进入磁场过程中通过ab截面的电量;
(4)线框穿过磁场的运动过程产生的焦耳热.
分析:(1)对Q同轴转动,角速度相等,则线速度之比为1:2,所以线框与物体的速度之比v2:v1=1:2,从而得出线框和物体在任一时刻的动能之比.
(2)当线框做匀速运动时,物块和线框均处于平衡状态,根据共点力平衡,结合闭合电路欧姆定律以及切割产生的电动势公式,通过两个拉力的关系T1r1=T2r2,求出ad边从磁场上边缘穿出时速度的大小.
(3)根据q=N
求出线框进入磁场过程中通过ab截面的电量.从线框刚刚开始运动到ad边刚要进入磁场,对系统运用动能定理,抓住线框与物块动能的关系,求出ad刚进入磁场时线框动能的大小.
(4)从初状态到线框刚刚完全出磁场,运用能量守恒定律,求出线框穿过磁场的运动过程产生的焦耳热.
(2)当线框做匀速运动时,物块和线框均处于平衡状态,根据共点力平衡,结合闭合电路欧姆定律以及切割产生的电动势公式,通过两个拉力的关系T1r1=T2r2,求出ad边从磁场上边缘穿出时速度的大小.
(3)根据q=N
| △Φ |
| R |
(4)从初状态到线框刚刚完全出磁场,运用能量守恒定律,求出线框穿过磁场的运动过程产生的焦耳热.
解答:解:(1)对Q同轴转动:所以线框与物体的速度之比v2:v1=1:2,
由EK=
mv2知:EK1:EK2=8:1
(2)由于线框匀速出磁场,
则对m1有:m1gsinθ-μm1gcosθ=T1,
对m2有:T2=m2g+BIL,
对Q有:T1r1=T2r2
联立并代入数据可得:v=
R=
(3)电量 q=It=
从线框刚刚开始运动到ad边刚要进入磁场,由动能定理得:(m1gsinθ-μm1gcomθ)×2L-m2gL=EK2+EK1-0
且8EK2=EK1将代入,整理可得线框刚刚进入磁场时,动能为EK2=
(4)从初状态到线框刚刚完全出磁场,由能的转化与守恒定律可得(m1gsinθ-μm1gcosθ)×6L-m2g×3L=Q+
m1(2v)2+
m2v2,
将数值代入,整理可得线框在整个运动过程中产生的焦耳热为:Q=3mgL-
.
答:(1)线框与物体在任一时刻的动能之比8:1.
(2)ad边从磁场上边缘穿出时速度的大小
.
(3)ad刚进入磁场时线框动能的大小
,通过ab截面的电量
.
(4)线框穿过磁场的运动过程产生的焦耳热为3mgL-
.
由EK=
| 1 |
| 2 |
(2)由于线框匀速出磁场,
则对m1有:m1gsinθ-μm1gcosθ=T1,
对m2有:T2=m2g+BIL,
对Q有:T1r1=T2r2
联立并代入数据可得:v=
| 2m1g(sinθ-μcosθ)-m2g |
| B2L2 |
| mgR |
| B2L2 |
(3)电量 q=It=
BL
| ||
| R |
从线框刚刚开始运动到ad边刚要进入磁场,由动能定理得:(m1gsinθ-μm1gcomθ)×2L-m2gL=EK2+EK1-0
且8EK2=EK1将代入,整理可得线框刚刚进入磁场时,动能为EK2=
| mgL |
| 9 |
(4)从初状态到线框刚刚完全出磁场,由能的转化与守恒定律可得(m1gsinθ-μm1gcosθ)×6L-m2g×3L=Q+
| 1 |
| 2 |
| 1 |
| 2 |
将数值代入,整理可得线框在整个运动过程中产生的焦耳热为:Q=3mgL-
| 9m3g2R2 |
| 2B4L4 |
答:(1)线框与物体在任一时刻的动能之比8:1.
(2)ad边从磁场上边缘穿出时速度的大小
| mgR |
| B2L2 |
(3)ad刚进入磁场时线框动能的大小
| mgL |
| 9 |
BL
| ||
| R |
(4)线框穿过磁场的运动过程产生的焦耳热为3mgL-
| 9m3g2R2 |
| 2B4L4 |
点评:本题综合考查了牛顿第二定律、动能定理、能量守恒定律,综合性强,对学生能力要求较高,是一道难题,解题时注意物块与线框的速度关系,通过的位移关系.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
 如图所示,一边长L=10cm的正方形金属导体框abcd,从某一高度h m处开始竖直向下自由下落,其下边进入只有水平上边界的匀强磁场,磁感应强度B=1.0T.线框进入磁场时,线框平面保持与磁场垂直,线框底边保持水平.已知正方形线框abcd的质量m=0.1kg,电阻R=0.02Ω,自下边ab进入磁场直到上边cd也进入磁场时为止,整个线框恰好能够保持做匀速直线运动.若g=10m/s2,不计空气阻力,求:
如图所示,一边长L=10cm的正方形金属导体框abcd,从某一高度h m处开始竖直向下自由下落,其下边进入只有水平上边界的匀强磁场,磁感应强度B=1.0T.线框进入磁场时,线框平面保持与磁场垂直,线框底边保持水平.已知正方形线框abcd的质量m=0.1kg,电阻R=0.02Ω,自下边ab进入磁场直到上边cd也进入磁场时为止,整个线框恰好能够保持做匀速直线运动.若g=10m/s2,不计空气阻力,求: 如图所示,一边长L=0.2m,质量m1=0.5kg,电阻R=0.1Ω的正方形导体线框abcd,与一质量为m2=2kg的物块通过轻质细线跨过两定滑轮相连.起初ad边距磁场下边界为d1=0.8m,磁感应强度B=2.5T,磁场宽度d2=0.3m,物块放在倾角θ=53°的斜面上,物块与斜面间的动摩擦因数μ=0.5.现将物块由静止释放,经一段时间后发现当ad边从磁场上边缘穿出时,线框恰好做匀速运动.(g取10m/s,sin53°=0.8,cos53°=0.6)求:
如图所示,一边长L=0.2m,质量m1=0.5kg,电阻R=0.1Ω的正方形导体线框abcd,与一质量为m2=2kg的物块通过轻质细线跨过两定滑轮相连.起初ad边距磁场下边界为d1=0.8m,磁感应强度B=2.5T,磁场宽度d2=0.3m,物块放在倾角θ=53°的斜面上,物块与斜面间的动摩擦因数μ=0.5.现将物块由静止释放,经一段时间后发现当ad边从磁场上边缘穿出时,线框恰好做匀速运动.(g取10m/s,sin53°=0.8,cos53°=0.6)求:
 ,自下边ab进入磁场直到上边cd也进入磁场时为止,整个线框恰好能够保持做匀速直线运动。若g=10m/s2,不计空气阻力,求:
,自下边ab进入磁场直到上边cd也进入磁场时为止,整个线框恰好能够保持做匀速直线运动。若g=10m/s2,不计空气阻力,求: