题目内容
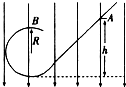 一个带电量为-q,质量为m的小球,从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,若仍从A点由静止释放该小球,则( )
一个带电量为-q,质量为m的小球,从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,若仍从A点由静止释放该小球,则( )分析:没有电场时,小球恰能通过轨道的最高点时恰好由重力提供向心力.加上电场时,运用动能定理分析到最高点时速度,研究向心力,判断能否通过最高点.
解答:解:A、加上电场后,根据动能定得:
mv2=(mg-Eq)h
所以当h取最大值时,小球动能最大,即小球运动到最低点时,动能最大,故A错误;
B、没有电场时,最高点速度设为v
则 mg=m
又根据机械能守恒定律
mg(h-2R)=m
解得h=
R
加上电场时,恰好过最高点需要的速度设为v′
则mg-qE=m
v′=
而由动能定理,得
mg(h-2R)-qE(h-2R)=
mv′2
v′=
说明小球仍恰好能过B点.故B错误;
C、由上,小球仍恰好过最高点,球与轨道间无作用力.故C错误;
D、小球运动过程中,除重力做功外,还有电场力做功,所以机械能不守恒,故D正确.
故选D.
| 1 |
| 2 |
所以当h取最大值时,小球动能最大,即小球运动到最低点时,动能最大,故A错误;
B、没有电场时,最高点速度设为v
则 mg=m
| v2 |
| R |
又根据机械能守恒定律
mg(h-2R)=m
| v2 |
| R |
解得h=
| 5 |
| 2 |
加上电场时,恰好过最高点需要的速度设为v′
则mg-qE=m
| v′2 |
| R |
v′=
|
而由动能定理,得
mg(h-2R)-qE(h-2R)=
| 1 |
| 2 |
v′=
|
说明小球仍恰好能过B点.故B错误;
C、由上,小球仍恰好过最高点,球与轨道间无作用力.故C错误;
D、小球运动过程中,除重力做功外,还有电场力做功,所以机械能不守恒,故D正确.
故选D.
点评:本题是动能定理和向心力知识的综合,关键是分析小球过最高点的临界速度.

练习册系列答案
相关题目
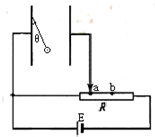
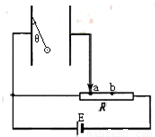
 竖直放置的一对平行金属板的左极板上,用长为l的轻质绝缘细线悬挂一个带电量为q质量为 m的小球,将平行金属板按如图所示的电路图连接.当滑动变阻器R在a位置时,绝缘线与左极板的夹角为θ1=30°,当将滑片缓慢地移动到b位置时,夹角为θ2=60°.两板间的距离大于l,重力加速度为g.问:
竖直放置的一对平行金属板的左极板上,用长为l的轻质绝缘细线悬挂一个带电量为q质量为 m的小球,将平行金属板按如图所示的电路图连接.当滑动变阻器R在a位置时,绝缘线与左极板的夹角为θ1=30°,当将滑片缓慢地移动到b位置时,夹角为θ2=60°.两板间的距离大于l,重力加速度为g.问:
 竖直放置的一对平行金属板的左极板上,用长为l的轻质绝缘细线悬挂一个带电量为q质量为 m的小球,将平行金属板按如图所示的电路图连接.当滑动变阻器R在a位置时,绝缘线与左极板的夹角为θ1=30°,当将滑片缓慢地移动到b位置时,夹角为θ2=60°.两板间的距离大于l,重力加速度为g.问:
竖直放置的一对平行金属板的左极板上,用长为l的轻质绝缘细线悬挂一个带电量为q质量为 m的小球,将平行金属板按如图所示的电路图连接.当滑动变阻器R在a位置时,绝缘线与左极板的夹角为θ1=30°,当将滑片缓慢地移动到b位置时,夹角为θ2=60°.两板间的距离大于l,重力加速度为g.问: