题目内容
15.汽车从静止开始做匀加速直线运动,那么从开始加速到2s末和3s末汽车通过的位移之比为( )| A. | 2:3 | B. | 4:9 | C. | 3:5 | D. | 1:9 |
分析 根据匀变速直线运动的位移时间公式,求出开始加速到2s末和3s末通过的位移之比.
解答 解:根据x=$\frac{1}{2}a{t}^{2}$知,时间之比为2:3,则位移之比为4:9,故B正确,A、C、D错误.
故选:B.
点评 解决本题的关键掌握匀变速直线运动的位移时间公式,并能灵活运用,基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
5.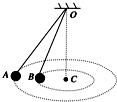 如图所示,两根轻绳的一端都固定于O点,另一端分别系两个相同的小铁球,两小球恰好在同一水平面内做匀速圆周运动,则( )
如图所示,两根轻绳的一端都固定于O点,另一端分别系两个相同的小铁球,两小球恰好在同一水平面内做匀速圆周运动,则( )
 如图所示,两根轻绳的一端都固定于O点,另一端分别系两个相同的小铁球,两小球恰好在同一水平面内做匀速圆周运动,则( )
如图所示,两根轻绳的一端都固定于O点,另一端分别系两个相同的小铁球,两小球恰好在同一水平面内做匀速圆周运动,则( )| A. | B球做匀速圆周运动的周期较大 | |
| B. | 它们所需的向心力跟轨道半径成正比 | |
| C. | A球做匀速圆周运动的线速度较大 | |
| D. | 两球受绳的拉力相等 |
6.若汽车的加速度方向与速度方向一致,当加速度减小时,则( )
| A. | 汽车的速度也减小 | |
| B. | 汽车的速度仍在增大 | |
| C. | 当加速度减小到零时,汽车静止 | |
| D. | 当加速度减小到零时,汽车的速度将减小 |
10.两个人负责安装一个炸药包,然后启爆,两个人分别控制两个相串联的开关.只有当两个人都撤出危险区,在安全区把开关接通时,炸药包才能爆炸.如果有一人未撤出危险区,开关没有接通,炸药包就不能启爆,这就是“与”的概念.如果用0表示不启爆,1表示启爆,用符号“×”表示“与”的运算符号,则下列运算式正确的是( )
| A. | 0×0=0,表示二人都不启爆,炸药包不爆炸 | |
| B. | 0×1=1,表示一人不启爆,另一人启爆,炸药包爆炸 | |
| C. | 1×0=1,表示一人启爆,另一人不启爆,炸药包爆炸 | |
| D. | 1×1=1,表示二人都启爆,炸药包爆炸 |
7.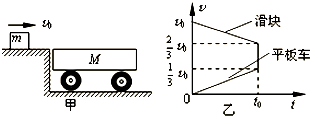 如图甲所示,光滑水平面上停放着一辆上表面粗糙的平板车,质量为M,一质量m的铁块以水平初速度v0滑到小车上,两物体开始运动,它们的速度随时间变化的图象如图乙所示(t0是滑块在车上运动的时间),则可以断定( )
如图甲所示,光滑水平面上停放着一辆上表面粗糙的平板车,质量为M,一质量m的铁块以水平初速度v0滑到小车上,两物体开始运动,它们的速度随时间变化的图象如图乙所示(t0是滑块在车上运动的时间),则可以断定( )
 如图甲所示,光滑水平面上停放着一辆上表面粗糙的平板车,质量为M,一质量m的铁块以水平初速度v0滑到小车上,两物体开始运动,它们的速度随时间变化的图象如图乙所示(t0是滑块在车上运动的时间),则可以断定( )
如图甲所示,光滑水平面上停放着一辆上表面粗糙的平板车,质量为M,一质量m的铁块以水平初速度v0滑到小车上,两物体开始运动,它们的速度随时间变化的图象如图乙所示(t0是滑块在车上运动的时间),则可以断定( )| A. | 铁块最终能与小车达到相对静止 | |
| B. | 铁块与小车的质量之比m:M=1:2 | |
| C. | 铁块与小车表面的动摩擦因数μ=$\frac{{v}_{0}}{3g{t}_{0}}$ | |
| D. | 平板车上表面的长度为$\frac{5{v}_{0}{t}_{0}}{6}$ |
5.如图所示,电路中的R1和R2相等,在滑动变阻器的滑片P自左至右滑动的过程中,AB间的总电阻将( )
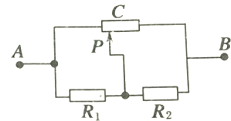

| A. | 逐渐增大 | B. | 先增大,后减小 | C. | 逐渐减小 | D. | 先减小,后增大 |
 如图所示为一架小型四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.无人机的质量为m=2kg,运动过程中所受空气阻力大小恒为f=4N,当无人机在地面上从静止开始,以最大升力竖直向上起飞,经时间t=4s时离地面的高度为h=48m,g取10m/s2.求:
如图所示为一架小型四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.无人机的质量为m=2kg,运动过程中所受空气阻力大小恒为f=4N,当无人机在地面上从静止开始,以最大升力竖直向上起飞,经时间t=4s时离地面的高度为h=48m,g取10m/s2.求: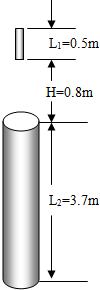 如图所示,直杆长L1=0.5m,圆筒高为L2=3.7m.直杆位于 圆筒正上方H=0.8m处.直杆从静止开始做自由落体运动,并能竖直穿越圆筒.试求(取g=10m/s2)
如图所示,直杆长L1=0.5m,圆筒高为L2=3.7m.直杆位于 圆筒正上方H=0.8m处.直杆从静止开始做自由落体运动,并能竖直穿越圆筒.试求(取g=10m/s2)