题目内容
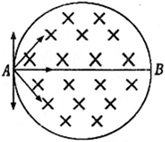 如图所示,一匀强磁场磁感应强度为B,方向垂直纸面向里,其边界是半径为R的圆,AB为圆的一直径,在A点有一粒子源向圆平面内的各个方向发射质量m、电量-q的粒子,粒子重力不计.
如图所示,一匀强磁场磁感应强度为B,方向垂直纸面向里,其边界是半径为R的圆,AB为圆的一直径,在A点有一粒子源向圆平面内的各个方向发射质量m、电量-q的粒子,粒子重力不计.(1)有一带电粒子以v1=
| 2qBR | m |
(2)若磁场的边界是绝缘弹性边界(粒子与边界碰撞后将以原速率反弹),某粒子沿半径方向射入磁场,经过2次碰撞后回到A点,则该粒子的速度为多大?
分析:(1)粒子进入磁场后由洛伦兹力提供向心力做匀速圆周运动,由牛顿第二定律求出轨迹的半径,由几何知识求解轨迹对应的圆心角α,由t=
T求解粒子在磁场中运动的时间.
(2)粒子沿半径方向射入磁场,经过2次碰撞后回到A点,画出粒子运动的轨迹,由几何知识求出轨迹的半径,即可求出该粒子的速度.
| α |
| 2π |
(2)粒子沿半径方向射入磁场,经过2次碰撞后回到A点,画出粒子运动的轨迹,由几何知识求出轨迹的半径,即可求出该粒子的速度.
解答:解:(1)由牛顿第二定律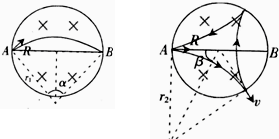
qv1B=m
又 v1=
解得 r1=2R
粒子的运动轨迹如左图所示,则得 α=
此粒子在磁场中运动的时间为 t=
T=
(2)粒子的运动轨迹如右图所示,则得 β=
则 r2=Rtanβ=
R
根据牛顿第二定律,有
qv2B=m
解得,v2=
答:(1)此粒子在磁场中运动的时间为
.
(2)该粒子的速度为
.

qv1B=m
| ||
| r1 |
又 v1=
| 2qBR |
| m |
解得 r1=2R
粒子的运动轨迹如左图所示,则得 α=
| π |
| 3 |
此粒子在磁场中运动的时间为 t=
| α |
| 2π |
| πm |
| 3Bq |
(2)粒子的运动轨迹如右图所示,则得 β=
| π |
| 3 |
则 r2=Rtanβ=
| 3 |
根据牛顿第二定律,有
qv2B=m
| ||
| r2 |
解得,v2=
| ||
| m |
答:(1)此粒子在磁场中运动的时间为
| πm |
| 3Bq |
(2)该粒子的速度为
| ||
| m |
点评:本题的解题关键是画出粒子的运动轨迹,由几何知识求解轨迹的半径.

练习册系列答案
相关题目
 (2009?枣庄一模)如图所示,一匀强磁场磁感应强度为B;方向向里,其边界是半径为R的圆,AB为圆的一直径.在A点有一粒子源向圆平面内的各个方向发射质量m、电量-q的粒子,粒子重力不计.
(2009?枣庄一模)如图所示,一匀强磁场磁感应强度为B;方向向里,其边界是半径为R的圆,AB为圆的一直径.在A点有一粒子源向圆平面内的各个方向发射质量m、电量-q的粒子,粒子重力不计.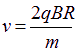 的速度垂直磁场进入圆形区域,恰从B点射出.求此粒子在磁场中运动的时间.
的速度垂直磁场进入圆形区域,恰从B点射出.求此粒子在磁场中运动的时间.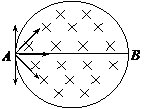

 的速度垂直磁场进入圆形区域,恰从B点射出.求此粒子在磁场中运动的时间.
的速度垂直磁场进入圆形区域,恰从B点射出.求此粒子在磁场中运动的时间.