题目内容
 如图,真空中固定着一个电量为Q的正点电荷A,另有一点电荷B在A正下方h所在水平面内做半径为r的匀速圆周运动,电荷B的质量为m,重力加速度为g,静电力常量为k,求:
如图,真空中固定着一个电量为Q的正点电荷A,另有一点电荷B在A正下方h所在水平面内做半径为r的匀速圆周运动,电荷B的质量为m,重力加速度为g,静电力常量为k,求:(1)电荷B的电性和电量;
(2)电荷B的运动周期.
分析:(1)点电荷B在水平面内做匀速圆周运动,由重力和库仑力的合力提供向心力,即可判断电荷B的电性.根据牛顿第二定律列式求解电量.
(2)根据重力mg和库仑力F的合力提供向心力,列式求解周期.
(2)根据重力mg和库仑力F的合力提供向心力,列式求解周期.
解答: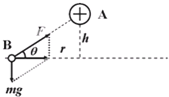 解:(1)对电荷B受力分析,如图,重力mg和库仑力F的合力提供向心力,
解:(1)对电荷B受力分析,如图,重力mg和库仑力F的合力提供向心力,
由受力分析知电荷B带负电,设其带电量为q,则根据牛顿第二定律得:
k
=
…①
由几何关系知:
sinθ=
…②
由①②得:q=
,电性为负.
(2)由重力mg和库仑力F的合力提供向心力,设B的周期为T,则得:
=m
r…③
由几何关系知:
tanθ=
… ④
由③④得:T=2π
答:(1)电荷B带负电,其电量为
;
(2)电荷B的运动周期为2π
.
 解:(1)对电荷B受力分析,如图,重力mg和库仑力F的合力提供向心力,
解:(1)对电荷B受力分析,如图,重力mg和库仑力F的合力提供向心力,由受力分析知电荷B带负电,设其带电量为q,则根据牛顿第二定律得:
k
| h2+r2 |
| mg |
| sinθ |
由几何关系知:
sinθ=
| h | ||
|
由①②得:q=
mg(h2+r2)
| ||
| khQ |
(2)由重力mg和库仑力F的合力提供向心力,设B的周期为T,则得:
| mg |
| tanθ |
| 4π2 |
| T2 |
由几何关系知:
tanθ=
| h |
| r |
由③④得:T=2π
|
答:(1)电荷B带负电,其电量为
mg(h2+r2)
| ||
| khQ |
(2)电荷B的运动周期为2π
|
点评:本题是圆锥摆问题,关键分析受力情况,确定电荷B向心力的来源,由牛顿第二定律和圆周运动的规律结合求解.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
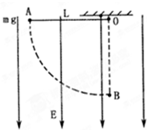
 如图在真空中存在着竖直向下的匀强电场,其场强为E,一根绝缘细线长为L,它一端固定在图中的O点,另一端固定有一个质量为m,带电量为q的点电荷,将该点电荷拉至图示的位置A从静止释放.求:
如图在真空中存在着竖直向下的匀强电场,其场强为E,一根绝缘细线长为L,它一端固定在图中的O点,另一端固定有一个质量为m,带电量为q的点电荷,将该点电荷拉至图示的位置A从静止释放.求: