题目内容
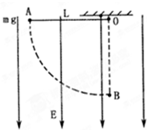
 如图在真空中存在着竖直向下的匀强电场,其场强为E,一根绝缘细线长为L,它一端固定在图中的O点,另一端固定有一个质量为m,带电量为q的点电荷,将该点电荷拉至图示的位置A从静止释放.求:
如图在真空中存在着竖直向下的匀强电场,其场强为E,一根绝缘细线长为L,它一端固定在图中的O点,另一端固定有一个质量为m,带电量为q的点电荷,将该点电荷拉至图示的位置A从静止释放.求:(1)点电荷运动到O点正下方B点时的速度大小
(2)此刻细线对点电荷拉力大小为多少?
分析:(1)在电荷向下运动过程中,重力与电场力对小球做功,绳子的拉力不做功,由动能定理可以求出电荷运动到最低点时的速度.
(2)小球做圆周运动,重力、电场力、绳子拉力的合力提供向心力,由牛顿第二定律可以求出绳子的拉力.
(2)小球做圆周运动,重力、电场力、绳子拉力的合力提供向心力,由牛顿第二定律可以求出绳子的拉力.
解答:解:(1)从A到B过程,由动能定理得:
mgL+qEL=
mv2-0,
小球到达B时的速度v=
;
(2)在B点,由牛顿第二定律得:
T-mg-qE=m
,解得:T=3(mg+qE);
答:(1)点电荷运动到O点正下方B点时的速度大小为
;
(2)此刻细线对点电荷拉力大小为3(mg+qE).
mgL+qEL=
| 1 |
| 2 |
小球到达B时的速度v=
|
(2)在B点,由牛顿第二定律得:
T-mg-qE=m
| v2 |
| L |
答:(1)点电荷运动到O点正下方B点时的速度大小为
|
(2)此刻细线对点电荷拉力大小为3(mg+qE).
点评:对小球正确受力分析、应用动能定理及牛顿第二定律即可正确解题.

练习册系列答案
相关题目