题目内容
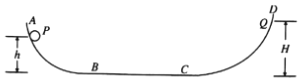
【题目】如图,一个上下都与大气相通的竖直放置的圆筒,中间用两个活塞A和B封住一定质量的气体。A、B都可沿圆筒无摩擦上下滑动且不漏气,B与轻质弹簧相连,轻质弹簧另一端固定在水平面上,初始时A、B间的距离为l0。现用竖直向下的力F压A,使之缓慢向下移动一段距离后,保持平衡(气体温度保持不变)。已知A的质量不计,B有一定质量,直圆筒内部的横截面积S = 0.01 m2,弹簧劲度系数k = 5×103 N/m,大气压p0 = 1×105 Pa,l0 = 0.6 m,F = 500 N。求A下移的距离。

【答案】l=0.3m
【解析】
由于A的质量可不计,初态时,封闭气体的压强等于大气压,以B为研究对象,求出弹簧的压缩量。当用力压A时,再以B为研究对象,求出弹簧的弹力,由胡克定律求出弹簧的压缩量,根据玻意耳定律求出活塞A向下移动的距离。
设A下移距离为l,B下移距离为x,由玻意耳定律得
![]()
根据胡克定律得F=kx
联立解得:l=0.3 m

练习册系列答案
相关题目