题目内容
19.如图所示,x轴上方有一匀强磁场,磁感应强度的方向垂直于纸面向里,大小为B,x轴下方有一匀强电场,电场强度的大小为E,方向与y轴的夹角θ为45°且斜向上方.现有一质量为m电量为q的正离子,以速度v0由y轴上的A点沿y轴正方向射入磁场,该离子在磁场中运动一段时间后从x轴上的C点进入电场区域,该离子经C点时的速度方向与x轴夹角为45°.不计离子的重力,设磁场区域和电场区域足够大.求:
(1)C点的坐标;
(2)离子从A点出发到第三次穿越x轴时的运动时间;
(3)离子第四次穿越x轴时速度的大小及速度方向与电场方向的夹角.
分析 (1)带电粒子在匀强磁场中在洛仑兹力作用下做匀速圆周运动,由牛顿第二定律求出轨迹半径.画出粒子运动的轨迹,由几何知识求出C点的坐标;
(2)根据运动轨迹的几何关系,来确定圆心角,并结合周期公式与牛顿第二定律、运动学公式,即可求解;
(3)根据粒子做类平抛运动处理规律,由运动的分解,并结合运动学公式,即可求解.
解答 解:(1)磁场中带电粒子在洛仑兹力作用下做圆周运动,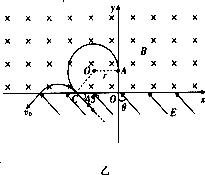
由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{r}$,
解得:r=$\frac{m{v}_{0}}{qB}$,
由几何知识知,xC=-(r+rcos450)=-$\frac{(2+\sqrt{2})m{v}_{0}}{2qB}$,
故,C点坐标为(-$\frac{(2+\sqrt{2})m{v}_{0}}{2qB}$,0).
(2)粒子做圆周运动的周期:T=$\frac{2πm}{qB}$,
设粒子从A到C的时间为t1,由几何知识知:t1=$\frac{5}{8}$T=$\frac{5πm}{4qB}$,
设粒子从进入电场到返回C的时间为t2,其在电场中做匀变速运动,
由牛顿第二定律和运动学公式,有:qE=ma,2v0=at2,
解得:t2=$\frac{2m{v}_{0}}{qE}$,
设粒子再次进入磁场后在磁场中运动的时间为t3,由题意得:t3=$\frac{1}{4}$T=$\frac{πm}{2qB}$,
粒子从A点到第三次穿越x轴的时间为:t=t1+t2+t3=$\frac{7πm}{4qB}$+$\frac{2m{v}_{0}}{qE}$;
(3)粒子第一次经过x轴后做匀减速直线运动,速度减为零后又做匀加速直线运动,
以和离开时相同的速率第二次进入磁场,然后做匀速圆周运动,离子从第三次过x轴到第四次过x轴的过程在电场中做类平抛运动,
设沿着v0的方向为x′轴,离子沿x′轴做匀速直线运动,运动轨迹如图所示:
设沿着电场的方向为y′轴,离子沿y′轴做初速为零的匀变速直线运动x1=v0t ①
y1=$\frac{1}{2}$$\frac{qE}{m}$t2 ②
vy′=$\frac{qE}{m}$ ③
由图中几何关系知:$\frac{{y}_{1}}{{x}_{1}}$=tan45° ④
设离子第四次穿越x轴时速度的大小为v,速度方向与电场方向的夹角为β,
v=$\sqrt{{v}_{0}^{2}+{v′}_{y}^{2}}$ ⑤
tanβ=$\frac{{v}_{0}}{{v}_{y}′}$ ⑥
由①~⑥式得解得:v=$\sqrt{5}$v0,β=arctan$\frac{1}{2}$;
答:(1)C点的坐标为(-$\frac{(2+\sqrt{2})m{v}_{0}}{2qB}$,0);
(2)离子从A点出发到第三次穿越x轴时的运动时间为$\frac{7πm}{4qB}$+$\frac{2m{v}_{0}}{qE}$;
(3)离子第四次穿越x轴时速度的大小为$\sqrt{5}$v0,速度方向与电场方向的夹角为arctan$\frac{1}{2}$.
点评 该题是一道综合性较强的题,解决此类问题的方法及关键:
(1)寻找突破口(程序法:顺藤摸瓜,逆向思维法:反其道而行之.
(2)画好轨迹图(在画图的基础上特别注意运用几何知识寻找关系.
(3)巧选力学规律(力和运动的关系:根据带电粒子所受的力,运用牛顿第二定律并结合运动学规律求解.功能关系:根据场力及其它外力对带电粒子做功引起的能量变化或全过程中的功能关系,从而可确定带电粒子的运动情况,这条线索不但适用于均匀场,也适用于非均匀场.因此要熟悉各种力做功的特点.解决这类题时一定要注意临界条件的挖掘:如“恰好”、“最大”、“最多”、“至少”…等关键词,往往是解题的突破口.

 阅读快车系列答案
阅读快车系列答案| A. | 质点是一个科学和理想的物理模型 | |
| B. | 地球很大,因此在任何情况下都不可视为质点 | |
| C. | 利用北斗导航系统确定“辽宁舰”在太平洋上的位置时,可视为质点 | |
| D. | 研究J31战机从某基地飞往钓鱼岛所需时间,可将J31战机视为质点 |

| A. | 路端电压变小 | B. | 电流表的示数变大 | ||
| C. | 电源内阻消耗的功率变大 | D. | 电路的总电阻变大 |
 两个固定的等量异号点电荷所产生电场等势面如图中虚线所示,一带负电的粒子以某一速度从图中A点沿图示方向进入电场在纸面内飞行,最后离开电场,粒子只受静电力作用,则粒子在电场中( )
两个固定的等量异号点电荷所产生电场等势面如图中虚线所示,一带负电的粒子以某一速度从图中A点沿图示方向进入电场在纸面内飞行,最后离开电场,粒子只受静电力作用,则粒子在电场中( )| A. | 做直线运动,电势能先变小后变大 | B. | 做直线运动,电势能先变大后变小 | ||
| C. | 做曲线运动,电势能先变小后变大 | D. | 做曲线运动,电势能先变大后变小 |
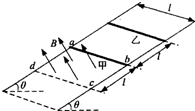 如图所示,电阻不计的足够长光滑平行金属导轨与水平面夹角为θ,导轨间距为l,轨道所在平面的正方形区域如耐内存在着有界匀强磁场,磁感应强度大小为B,方向垂直于导轨平面向上.电阻相同、质量均为m的两根相同金属杆甲和乙放置在导轨上,甲金属杆恰好处在磁场的上边界处,甲、乙相距也为l.在静止释放两金属杆的同时,对甲施加一沿导轨平面且垂直甲金属杆的外力,使甲在沿导轨向下的运动过程中始终以加速度a=gsinθ做匀加速直线运动,金属杆乙剐进入磁场时即做匀速运动.
如图所示,电阻不计的足够长光滑平行金属导轨与水平面夹角为θ,导轨间距为l,轨道所在平面的正方形区域如耐内存在着有界匀强磁场,磁感应强度大小为B,方向垂直于导轨平面向上.电阻相同、质量均为m的两根相同金属杆甲和乙放置在导轨上,甲金属杆恰好处在磁场的上边界处,甲、乙相距也为l.在静止释放两金属杆的同时,对甲施加一沿导轨平面且垂直甲金属杆的外力,使甲在沿导轨向下的运动过程中始终以加速度a=gsinθ做匀加速直线运动,金属杆乙剐进入磁场时即做匀速运动. 如图所示为某一简谐横波在t=0时刻的波形图,由此可知该波沿x轴正方向方向传播,该时刻a、b、c三点加速度最大的是c点,从这时刻开始,第一次最快回到平衡位置的是c点.若t=0.02s时质点c第一次到达波谷处,则此波的波速为100m/s.
如图所示为某一简谐横波在t=0时刻的波形图,由此可知该波沿x轴正方向方向传播,该时刻a、b、c三点加速度最大的是c点,从这时刻开始,第一次最快回到平衡位置的是c点.若t=0.02s时质点c第一次到达波谷处,则此波的波速为100m/s.
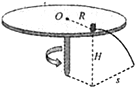 如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5 m,离水平地面的高度H=1.25m,物块与转台间的动摩擦因数为0.2.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2 求:
如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5 m,离水平地面的高度H=1.25m,物块与转台间的动摩擦因数为0.2.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2 求: