题目内容
9.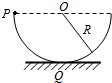 如图,一半径为R,质量为M的半圆形轨道竖直放置,轨道两端等高,质量为m的质点自轨道端点E由静止开始向下滑到最低点Q,该过程中克服摩擦力所做的功为W=$\frac{1}{2}$mgR,质点经最低点时对圆轨的压力为F1,圆轨受地面的支持力为F2,重力加速度大小为g,则( )
如图,一半径为R,质量为M的半圆形轨道竖直放置,轨道两端等高,质量为m的质点自轨道端点E由静止开始向下滑到最低点Q,该过程中克服摩擦力所做的功为W=$\frac{1}{2}$mgR,质点经最低点时对圆轨的压力为F1,圆轨受地面的支持力为F2,重力加速度大小为g,则( )| A. | F1=2mg | B. | F1>3mg | C. | F1=(M+m)g | D. | F1>(M+3m)g |
分析 先由动能定理求解出质点通过最低点时的速度.质点经过最低点时,由重力和轨道的支持力提供向心力,由牛顿运动定律求出质点对轨道的压力,再对轨道研究,由平衡条件求出支持力F2.
解答 解:质点下滑的过程中,由动能定理得:
mgR-W=$\frac{1}{2}m{v}^{2}$
据题W=$\frac{1}{2}$mgR,解得 v=$\sqrt{gR}$
质点经过最低点时,由重力和轨道的支持力提供向心力,由牛顿第二定律得:
F1′-mg=m$\frac{{v}^{2}}{R}$
可得 F1′=2mg
根据牛顿第二定律得,质点经最低点时对圆轨的压力为 F1=F1′=2mg
对轨道,由平衡条件得:圆轨受地面的支持力为 F2=Mg+F1=(M+2m)g
故选:A.
点评 本题考查动能定理的应用及向心力公式,要注意正确受力分析,明确指向圆心的合力提供圆周运动的向心力,知道动能定理是求解速度常用的方法.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
19. 一个物体受到的合力F如图所示,该力的大小不变,方向随时间t周期性变化,正力表示力的方向水平向东,负力表示力的方向水平向西,力的总作用时间足够长,将物体在下面哪些时刻由静止释放,物体可以运动到出发点的西边且离出发点很远的地方( )
一个物体受到的合力F如图所示,该力的大小不变,方向随时间t周期性变化,正力表示力的方向水平向东,负力表示力的方向水平向西,力的总作用时间足够长,将物体在下面哪些时刻由静止释放,物体可以运动到出发点的西边且离出发点很远的地方( )
 一个物体受到的合力F如图所示,该力的大小不变,方向随时间t周期性变化,正力表示力的方向水平向东,负力表示力的方向水平向西,力的总作用时间足够长,将物体在下面哪些时刻由静止释放,物体可以运动到出发点的西边且离出发点很远的地方( )
一个物体受到的合力F如图所示,该力的大小不变,方向随时间t周期性变化,正力表示力的方向水平向东,负力表示力的方向水平向西,力的总作用时间足够长,将物体在下面哪些时刻由静止释放,物体可以运动到出发点的西边且离出发点很远的地方( )| A. | t=t1 | B. | $t=\frac{1}{2}{t_1}$ | C. | $t=\frac{2}{3}{t_1}$ | D. | $t=\frac{1}{3}{t_1}$ |
17.电动势为E,内电阻为r的电池给电阻负载供电.下列说法中正确的是( )
| A. | 负载电阻越大,电池供电效率就越大 | |
| B. | 负载电阻越大,电池的路端电压就越大 | |
| C. | 电池输出电压越大,输出功率就越大 | |
| D. | 电池的输出电流越大,其输出功率就越大 |
15.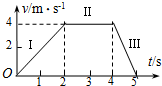 如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段.下列说法中正确的是( )
如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段.下列说法中正确的是( )
 如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段.下列说法中正确的是( )
如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段.下列说法中正确的是( )| A. | 第1s与第3s的速度方向相同 | |
| B. | 第1s的加速度大于第5s的加速度 | |
| C. | 第Ⅰ段与第Ⅲ段的平均速度相等 | |
| D. | 第Ⅰ段和第Ⅲ段的加速度与速度的方向都相同 |
16.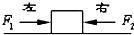 如图,一木块放在水平桌面上,在水平方向共受到三个力,即F1、F2和桌面的摩擦力作用,木块处于静止状态.其中F1=10N,F2=2N,方向如图所示.现撤去力F1,则( )
如图,一木块放在水平桌面上,在水平方向共受到三个力,即F1、F2和桌面的摩擦力作用,木块处于静止状态.其中F1=10N,F2=2N,方向如图所示.现撤去力F1,则( )
 如图,一木块放在水平桌面上,在水平方向共受到三个力,即F1、F2和桌面的摩擦力作用,木块处于静止状态.其中F1=10N,F2=2N,方向如图所示.现撤去力F1,则( )
如图,一木块放在水平桌面上,在水平方向共受到三个力,即F1、F2和桌面的摩擦力作用,木块处于静止状态.其中F1=10N,F2=2N,方向如图所示.现撤去力F1,则( )| A. | 木块受摩擦力为8N,方向向左 | B. | 木块受摩擦力为6N,方向向左 | ||
| C. | 木块受摩擦力为2N,方向向右 | D. | 木块所受合力为2N,方向向右 |
 如图所示,a、b、c是匀强电场中的三点,并构成一等边三角形.每边长L=$\sqrt{21}$cm,将一带电荷量q=-2×10-6C的电荷从a点移到b点,电场力做功Wab=-1.2×10-5J;若将同一点电荷从a点移到c点,电场力做功Wac=6×10-6J,试求匀强电场的电场强度大小E.
如图所示,a、b、c是匀强电场中的三点,并构成一等边三角形.每边长L=$\sqrt{21}$cm,将一带电荷量q=-2×10-6C的电荷从a点移到b点,电场力做功Wab=-1.2×10-5J;若将同一点电荷从a点移到c点,电场力做功Wac=6×10-6J,试求匀强电场的电场强度大小E.