题目内容
【题目】如图甲所示,ABCD为一足够长的光滑绝缘斜面,EFGH范围内存在方向垂直斜面向上的匀强磁场,磁场边界EF、HG与斜面底边AB平行。一正方形金属框abcd放在斜面上,ab边平行于磁场边界。现使金属框从斜面上某处由静止释放,金属框从开始运动到cd边离开磁场的过程中,其运动的v—t图象如图乙所示。已知金属框电阻![]() ,质量m=0. 04kg,重力加速度g=10m/s2,求:
,质量m=0. 04kg,重力加速度g=10m/s2,求:
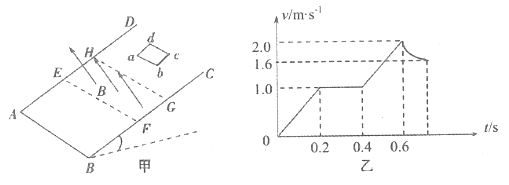
(1)磁场区域的磁感应强度B和宽度d;
(2)金属框穿过磁场过程中产生的焦耳热Q;
(3)金属框出磁场EF边界过程中通过金属框截面的电量q和所用时间![]() 。
。
【答案】(1)2T,0.5m(2)0.1088J(3)0.1C,0.12s
【解析】
(1)由图乙可知,在00.2s内金属框做匀加速运动,经t1=0.2s速度v1=1.0m/s,
加速度a=![]()
a=5m/s2
设斜面的倾角为![]() ,金属框边长为l0,由牛顿第二定律有mgsin
,金属框边长为l0,由牛顿第二定律有mgsin![]() =ma1
=ma1
解得sin![]() =0.5
=0.5
在0.2s0.4s内金属框勾速进入磁场,则l0=v1t2
l0=0.2m
有E1=Bl0v1
L1=![]()
F=Bl0I1
由F=mgsin![]()
得B=2T
在0.4s0.6s内,金属框在磁场中继续以a=5m/s2的加速度做匀加速运动,由图乙可知运动位移![]()
得x3=0.3m
则磁场的宽度d=l0+x3=0.5m
(2)金属框从进入磁场到离开磁场的过程中,由功能关系:mg·sin![]() (d+l0)=
(d+l0)=![]()
得Q=0.1088J
(3)金属框出磁场过程中,有:![]()
![]()
![]()
得![]()
Q=0.1C
mgsin![]() ·t4-Bl0q=mv3-mv2
·t4-Bl0q=mv3-mv2
得t4=0.12s

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目