题目内容
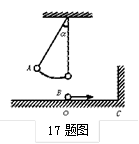
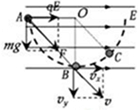
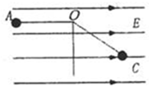 如图所示,摆长为L的不可伸长绝缘细线,一端固定在O点,另一端系一质量为m,带电荷量为+q小球,整个装置处于方向水平向右的匀强电场中,场强大小为E=mg/q,小球的平衡位置在C点,开始时让小球位于与O点同一水平高度的A点,且摆线拉直,然后无初速释放摆球,当小球经过O点正下方B点(图中未画出)的瞬间,因受细线的拉力作用,速度的竖直分量突变为0,水平分量不变.求:
如图所示,摆长为L的不可伸长绝缘细线,一端固定在O点,另一端系一质量为m,带电荷量为+q小球,整个装置处于方向水平向右的匀强电场中,场强大小为E=mg/q,小球的平衡位置在C点,开始时让小球位于与O点同一水平高度的A点,且摆线拉直,然后无初速释放摆球,当小球经过O点正下方B点(图中未画出)的瞬间,因受细线的拉力作用,速度的竖直分量突变为0,水平分量不变.求:(1)小球到达最低时速度的大小及方向.
(2)小球到达C点时细线对小球拉力的大小.(用m、g、L表示计算结果)
分析:(1)粒子受到的重力等于电场力,两个力的合力与水平方向成45度,故粒子做初速度为零的匀加速直线运动;对从A到最低点过程运用动能定理列式求解即可;
(2)小球在经过最低点B的瞬间,因受线的拉力作用,其速度的竖直分量vy突变为零,水平分量vx没有变化;从最低点到C点过程运用动能定理列式求出速度,再根据牛顿第二定律列式求解拉力.
(2)小球在经过最低点B的瞬间,因受线的拉力作用,其速度的竖直分量vy突变为零,水平分量vx没有变化;从最低点到C点过程运用动能定理列式求出速度,再根据牛顿第二定律列式求解拉力.
解答:解:(1)小球由A点沿着直线做初速度为零的匀加速运动到达O点正下方的B点.由动能定理得:
qEL+mgL=
mv2
解得
v=2
方向与竖直方向成45°角.
(2)小球在经过最低点B的瞬间,因受线的拉力作用,其速度的竖直分量vy突变为零,水平分量vx没有变化
vx=vcos45°=
小球在经过最低点B后做圆周运动到达C,OC与竖直方向的夹角为45°
qEL?sin45°-mgL(1-cos45°)=
m
-
m
根据牛顿第二定律,有
F-
mg=m
解得
F=3
mg
答:(1)小球到达最低时速度的大小为2
,方向与竖直方向成45°角;
(2)小球到达C点时细线对小球拉力的大小3
mg.
qEL+mgL=
| 1 |
| 2 |
解得
v=2
| gL |
方向与竖直方向成45°角.
(2)小球在经过最低点B的瞬间,因受线的拉力作用,其速度的竖直分量vy突变为零,水平分量vx没有变化

vx=vcos45°=
| 2gL |
小球在经过最低点B后做圆周运动到达C,OC与竖直方向的夹角为45°
qEL?sin45°-mgL(1-cos45°)=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 B |
根据牛顿第二定律,有
F-
| 2 |
| ||
| L |
解得
F=3
| 2 |
答:(1)小球到达最低时速度的大小为2
| gL |
(2)小球到达C点时细线对小球拉力的大小3
| 2 |
点评:本题关键分析清楚粒子的运动规律,然后结合运动的合成与分解、动能定理、牛顿第二定律列式求解.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
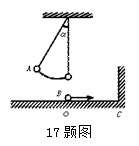
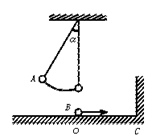
 如图所示,摆长为L的单摆,当摆球由A经平衡位置O向右运动的瞬间,另一小球B以速度v同时通过平衡位置向右运动,B与水平面无摩擦,与竖直墙壁碰撞无能量损失,问OC间距离x满足什么条件,才能使B返回时与A球相遇?
如图所示,摆长为L的单摆,当摆球由A经平衡位置O向右运动的瞬间,另一小球B以速度v同时通过平衡位置向右运动,B与水平面无摩擦,与竖直墙壁碰撞无能量损失,问OC间距离x满足什么条件,才能使B返回时与A球相遇?