题目内容
【题目】如图所示,一装满水的水槽放在太阳光下,将平面镜M斜放入水中,调整其倾斜角度,使一束太阳光从O点经水面折射和平面镜反射,然后经水面折射回到空气中,最后射到槽左侧上方的屏幕N上,即可观察到彩色光带.如果逐渐增大平面镜的倾角θ,各色光将陆续消失.已知所有光线均在同一竖直平面.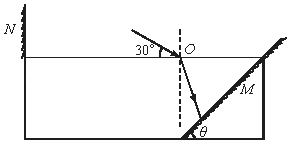
(i)从屏幕上最后消失的是哪种色光?(不需要解释)
(ii)如果射向水槽的光线与水面成30°,当平面镜M与水平面夹角θ=45°时,屏幕上的彩色光带恰好全部消失.求:对于最后消失的那种色光,水的折射率.
【答案】解:(i)逐渐增大平面镜的倾角θ,反射光线逆时针转动,反射光线射到水面的入射角增大,由于红光的临界角最大,所以红光的入射角最后达到临界角,最后发生全反射,故从屏幕上最后消失的是红色光.
(ii)画出如图所示的光路图.
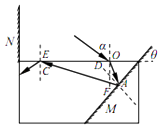
入射角 α=60° ①
OA是入射到平面镜上的光线,AD是法线,设∠AOF=β,∠OAD=γ.
由几何关系得:
β+γ=45° ②
C=β+2γ ③
由折射定律得: ![]() =n ④
=n ④
sinC= ![]() ⑤
⑤
由①~⑤联立解得 n= ![]()
答:(i)从屏幕上最后消失的是红色光.(ii)水的折射率是 ![]() .
.
【解析】(1)根据光的色散,光是由红橙黄绿蓝靛紫七种颜色的光组成,波长依次减小,频率依次增大。结合临界角和折射率之间的关系进行分析。
(2)画出光路图,红光发生全反射时,是镜面上的彩带,全部消失的时候。结合几何关系求解。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目